cho htg ABC nhọn ( AB nhỏ hơn AC). gọi M, N lần lượt là trung điểm của AB, AC. trên tia đối của tian MN lấy K sao cho NM= NK
a) c/m: tg AMN=tg KCN
b) c/m: AM song song KC và MB= KC
c)c/m: MN=\(\frac{1}{2}\) BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 2 2022
a: Xét tứ giác AMCD có
N là trung điểm của AC
N là trung điểm của MD
Do đó:AMCD là hình bình hành
Suy ra: CD//AM và CD=AM
=>CD//MB và CD=MB
b: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình
=>MN//BC và MN=1/2BC
26 tháng 8 2021
a) Xét tam giác AMN có
B là trung điểm của AM(AB=BM)
C là trung điểm của AN(AC=CN)
=> BC là đường trung bình của tam giác ABC
b) Xét tam giác AMJ có
B là trung điểm của AB(AB=BM)
I là trung điểm AJ(gt)
=> IB là đường trung bình của tam giác AMJ
=> IB//MJ(tính chất đường tb)
Ta có: IB//MJ(cmt)
Mà \(I\in BC\)(AI là đường trung truyến tam giác ABC)
=> BC//MJ
Ta có: MJ//BC(cmt)
MN//BC(cmt)
Theo tiên đề Ơ-clit ta suy ra:
M,J,N thẳng hàng
KV
4 tháng 12 2023
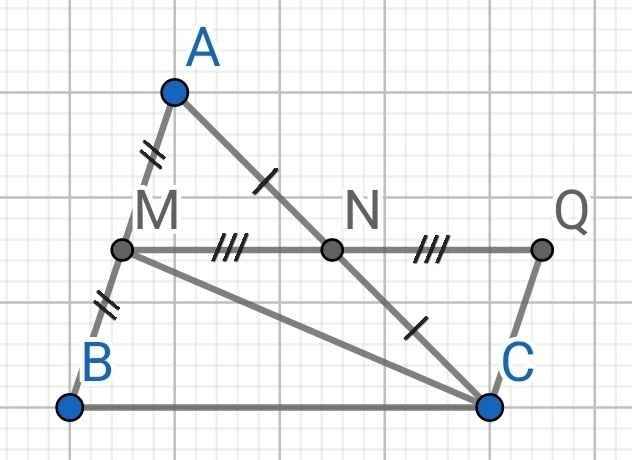
a) Xét ∆AMN và ∆CQN có:
AN = NC (do N là trung điểm của AC)
∠ANM = ∠CNQ (đối đỉnh)
NM = NQ (gt)
⇒ ∆AMN = ∆CQN (c-g-c)
b) Do ∆AMN = ∆CQN (cmt)
⇒ ∠MAN = ∠NCQ (hai góc tương ứng)
Mà ∠MAN và ∠NCQ là hai góc so le trong
⇒ AM // CQ
⇒ MB // CQ
c) Do ∆AMN = ∆CQN (cmt)
⇒ AM = CQ (hai cạnh tương ứng)
Mà AM = MB (do M là trung điểm của AB)
⇒ MB = CQ
Do BM // CQ (cmt)
⇒ ∠BMC = ∠QCM (so le trong)
Xét ∆BMC và ∆QCM có:
BM = CQ (cmt)
∠BMC = ∠QCM (cmt)
CM là cạnh chung
⇒ ∆BMC = ∆QCM (c-g-c)
⇒ BC = MQ (hai cạnh tương ứng)
Do NM = NQ (gt)
⇒ MN = 1/2 MQ
Mà BC = MQ (cmt)
⇒ MN = 1/2 BC