Tìm số nghiệm thuộc khoảng(−π;π)của phương trìnhsinx+ sin 2x= 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
5 tháng 7 2019
Đáp án A
Ta có c o s x + sin 2 x = 0 ⇔ cos x + 2 sin x cos x = 0 ⇔ [ cos x = 0 sin x = - 1 2 ⇔ [ x = π 2 + k π x = - π 6 + k 2 π x = 7 π 6 + k 2 π
Mà x ∈ - π ; π ⇒ x ∈ - π 2 ; π 2 ; - π 6 ; - 5 π 6 .
LP
0
PT
1
CM
24 tháng 10 2019
Đáp án C
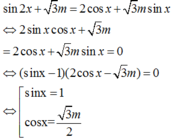
Để phương trình có một nghiệm duy nhất thuộc 0 ; π thì
CM
26 tháng 12 2017
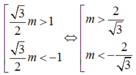
Đáp án B
TABLE f ( x ) = tan x + sin x + tan x − sin x − 3 tan x đổi dấu 1 lần trong 0 ; π ⇒ 1 nghiệm
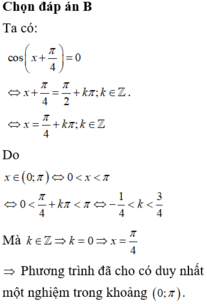
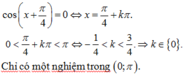
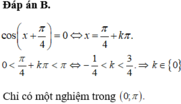
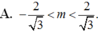
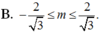
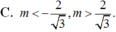
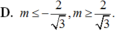
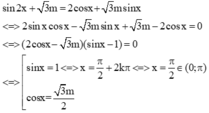
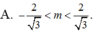
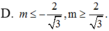
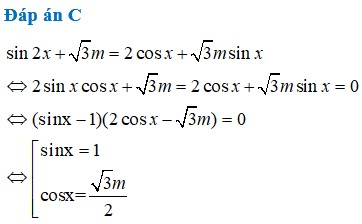
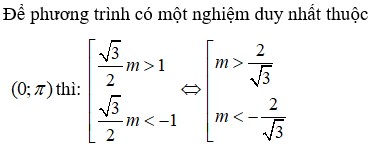
\(sin\left(x\right)+sin\left(2x\right)=0\)
\(\Leftrightarrow sin\left(x\right)+2sin\left(x\right)cos\left(x\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}sin\left(x\right)=0\\2cos\left(x\right)=-1\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}sin\left(x\right)=0\\cos\left(x\right)=-\frac{1}{2}\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=k\pi\\x=\pm\frac{2\pi}{3}+l2\pi\end{cases}};k,l\inℤ\)
mà \(x\in\left(-\pi,\pi\right)\)nên \(-\pi< k\pi< \pi\Rightarrow k=0\)
\(-\pi< \frac{\pm2}{3}\pi+l2\pi< \pi\Rightarrow l\in\left\{0,1\right\}\).
Vậy phương trình có \(3\)nghiệm thỏa mãn ycbt.