PC
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LP
0
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 11 2021
\(sin^2x-2m.sinx.cosx-sinx.cosx+2mcos^2x=0\)
\(\Leftrightarrow sinx\left(sinx-cosx\right)-2mcosx\left(sinx-cosx\right)=0\)
\(\Leftrightarrow\left(sinx-cosx\right)\left(sinx-2m.cosx\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}sinx=cosx\\sinx=2m.cosx\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}tanx=1\\tanx=2m\end{matrix}\right.\)
Do \(tanx=1\) ko có nghiệm đã cho nên \(tanx=2m\) phải có nghiệm trên khoảng đã cho
\(\Rightarrow tan\left(\dfrac{\pi}{4}\right)< 2m< tan\left(\dfrac{\pi}{3}\right)\)
\(\Rightarrow1< 2m< \sqrt[]{3}\)
\(\Rightarrow m\in\left(\dfrac{1}{2};\dfrac{\sqrt{3}}{2}\right)\) (hoặc có thể 1 đáp án là tập con của tập này cũng được)
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 12 2020
\(\Leftrightarrow1-2sin^2x+\left(2m-3\right)sinx+m-2=0\)
\(\Leftrightarrow2sin^2x-\left(2m-3\right)sinx-m+1=0\)
\(\Leftrightarrow2sin^2x+sinx-2\left(m-1\right)sinx-\left(m-1\right)=0\)
\(\Leftrightarrow sinx\left(2sinx+1\right)-\left(m-1\right)\left(2sinx+1\right)=0\)
\(\Leftrightarrow\left(2sinx+1\right)\left(sinx-m+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}sinx=-\dfrac{1}{2}\\sinx=m-1\end{matrix}\right.\)
Pt có đúng 2 nghiệm thuộc khoảng đã cho khi và chỉ khi:
\(\left\{{}\begin{matrix}m-1\ne-\dfrac{1}{2}\\-1\le m-1\le1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m\ne\dfrac{1}{2}\\0\le m\le2\end{matrix}\right.\)
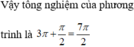
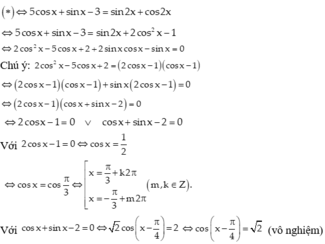
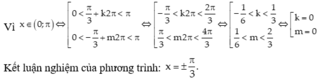
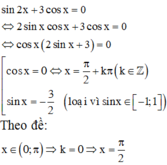
\(sin\left(x\right)+sin\left(2x\right)=0\)
\(\Leftrightarrow sin\left(x\right)+2sin\left(x\right)cos\left(x\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}sin\left(x\right)=0\\2cos\left(x\right)=-1\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}sin\left(x\right)=0\\cos\left(x\right)=-\frac{1}{2}\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=k\pi\\x=\pm\frac{2\pi}{3}+l2\pi\end{cases}};k,l\inℤ\)
mà \(x\in\left(-\pi,\pi\right)\)nên \(-\pi< k\pi< \pi\Rightarrow k=0\)
\(-\pi< \frac{\pm2}{3}\pi+l2\pi< \pi\Rightarrow l\in\left\{0,1\right\}\).
Vậy phương trình có \(3\)nghiệm thỏa mãn ycbt.