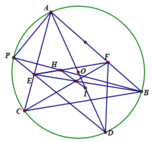
Cho tam giác ABC, trên các cạnh AB,AC lần lượt lấy D,E sao cho BD = BC = CE. CD giao BE tại F. Chứng minh rằng đường nối tâm nội tiếp I của tam giác ABC với trực tâm H của tam giác DEF đi qua trung điểm cung BAC của (ABC).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
27 tháng 7 2019
Bổ đề 1: Xét tam giác nhọn ABC, trên cạnh AB,AC lần lượt lấy D,E sao cho BD = CE. Gọi M,N lần lượt là trung điểm của DE,BC. Khi đó MN song song với đường phân giác trong của ^BAC.
Bổ đề 2: [Đường thẳng Gauss] Xét tứ giác lồi ABCD. AB giao CD tại X, AD giao BC tại Y. Gọi H,I,K thứ tự là trung điểm các đoạn AC,BD,XY. Khi đó H,I,K thẳng hàng.
Hai bổ đề trên khá quen thuộc, không trình bày ở đây.
Quay trở lại bài toán: Gọi V,J,L thứ tự là trung điểm của AI,DE,BC. Gọi JL cắt PQ tại R.
Dễ thấy V,J,L,R nằm trên đường thẳng Gauss của tứ giác AEID. Áp dụng bổ đề 1 ta thu được:
VR // AK. Mà V là trung điểm AI nên R là trung điểm IK (*)
Mặt khác ta thấy P,I,Q thẳng hàng, gọi PQ cắt (BID),(CIE) lần lượt tại S,T (S,T khác I), SB cắt TC tại F, Fx là phân giác ^BFC.
Ta có hai tam giác DIB,EIC có BD = CE, ^BID = ^EIC => (BID) = (EIC)
Theo tính chất của tâm nội tiếp thì SD = SP = SB, TE = TQ = TC. Từ đây SB = TC
Ta lại có biến đổi góc sau ^BFx = 1/2.^BFC = 900 - BDI/2 - ^CEI/2 = ^ADI/2 + ^AEI/2 - 900
= 1800 - ^DAE/2 - ^DIE/2 - 900 = ^EIT - ^DAE/2 = ^SBD - ^DAE/2 (= Góc hợp bởi AK và SB)
=> Fx // AK. Mà AK // RL nên Fx // RL. Áp dụng bổ đề 1 (với SB = TC) ta được R là trung điểm ST
Suy ra RS = RT => RP + SP = RQ + TQ => RP = RQ (Do SP = TQ) => R là trung điểm PQ (**)
Từ (*) và (**) suy ra KP = IQ. Như vậy KP + IK = IQ + IK => IP = QK (đpcm).
CM
8 tháng 3 2019
1). Gọi DE cắt (O) tại P khác D. Do AD là đường kính của (O), suy ra A P D ^ = 90 0 , mà A H E ^ = 90 0 ( do H E ∥ B C ⊥ H A ), nên tứ giác APEH nội tiếp.
Ta có A P H ^ = A E H ^ (góc nội tiếp)
= A C B ^ H E ∥ B C = A P B ^ (góc nội tiếp)
⇒ P H ≡ P B
2). Ta có H P ⊥ A C ⇒ A E H ^ = A H P ^ = A E P ^
Suy ra EA là phân giác ngoài đỉnh E của tam giác DEF
Tương tự FA là phân giác ngoài đỉnh F của tam giác DEF
Suy ra A là tâm đường tròn bàng tiếp ứng với đỉnh D của tam giác DEF
3). Do I là tâm nội tiếp nên EI là tia phân giác trong.
Mà EA là tia phân giác ngoài, suy ra E I ⊥ A C ⇒ E I ∥ H B
Tương tự F I ∥ H C ; E F ∥ B C ⇒ Δ I E F v à Δ H B C có cạnh tương ứng song song, nên BE; CF và IH đồng quy.
13 tháng 6 2023
a: Xét ΔADC và ΔAEB có
AD=AE
góc A chung
AC=AB
=>ΔADC=ΔAEB
b: Gọi giao của 3 đường trung trực trong ΔABC là O
=>OB=OC
Kẻ OK vuông góc BC, OK cắt DE tại M
=>OK là trung trực của BC
Xét ΔABC có AD/AB=AE/AC
nên DE//BC
=>OM vuông góc DE tạiM
Xét ΔOBD và ΔOCE có
OB=OC
góc OBD=góc OCE
BD=CE
=>ΔOBD=ΔOCE
=>OE=OD
=>OM là trung trực của DE
28 tháng 3 2020
Gọi M là trung điểm BC ; N là điểm đối xứng với H qua M.
M là trung điểm của BC và HN nên BNCH là hình bình hành
\(\Rightarrow NC//BH\)
Mà \(BH\perp AC\Rightarrow NC\perp AC\)hay AN là đường kính của đường tròn ( O )
Dễ thấy OM là đường trung bình \(\Delta AHN\) suy ra \(OM=\frac{1}{2}AH\)
M là trung điểm BC nên OM \(\perp\)BC
Xét \(\Delta AHG\)và \(\Delta OGM\)có :
\(\widehat{HAG}=\widehat{GMO}\); \(\frac{GM}{GA}=\frac{OM}{HA}=\frac{1}{2}\)
\(\Rightarrow\Delta AGH~\Delta MOG\left(c.g.c\right)\Rightarrow\widehat{AGH}=\widehat{MGO}\)hay H,G,O thẳng hàng
28 tháng 3 2020
gọi E,F,T lần lượt là trung điểm của AB,CD,BD
Đường thẳng ME cắt NF tại S
Vì AC = BD \(\Rightarrow EQFP\)là hình thoi \(\Rightarrow EF\perp PQ\)( 1 )
Xét \(\Delta TPQ\)và \(\Delta SEF\)có : \(ME\perp AB,TP//AB\)
Tương tự , \(NF\perp CD;\)\(TQ//CD\)
\(\Rightarrow\Delta TPQ~\Delta SEF\)( Góc có cạnh tương ứng vuông góc )
\(\Rightarrow\frac{SE}{SF}=\frac{TP}{TQ}=\frac{AB}{CD}\)
Mặt khác : \(\Delta MAB~\Delta NCD\Rightarrow\frac{AB}{CD}=\frac{ME}{NF}\)( tỉ số đường cao = tỉ số đồng dạng )
Suy ra : \(\frac{ME}{NF}=\frac{SE}{SF}\)\(\Rightarrow EF//MN\)( 2 )
Từ ( 1 ) và ( 2 ) suy ra \(MN\perp PQ\)
Bổ đề 1: Xét tứ giác MNPQ là tứ giác lồi có MP giao NQ tại R. Gọi H,K lần lượt là trực tâm của tam giác MRN;PRQ. U và V lần lượt là trung điểm của NP và MQ. Khi đó UV vuông góc với HK.
Bổ đề 2: Xét tam giác ABC nội tiếp (O), L là điểm chính giữa cung BAC. Lấy X thuộc cạnh AB, Y thuộc cạnh AC sao cho BX = CY. Khi đó LX = LY.
Hai bổ đề trên rất quen thuộc, các bạn tự chứng minh.
Giải bài toán: Đặt M,N thứ tự là trung điểm của BD,CE. Ta có BM = CN (= BD/2 = CE/2)
Gọi K là trung điểm cung BAC. Theo Bổ đề 2 thì KM = KN (1)
Dễ thấy ID = IC; IB = IE; BD = CE. Suy ra \(\Delta\)BID = \(\Delta\)EIC (c.c.c)
Hai tam giác trên có trung tuyến tương ứng là IM,IN. Do đó IM = IN (2)
Để ý rằng I là trực tâm của \(\Delta\)BFC. Áp dụng Bổ đề 1 vào tứ giác BDEC ta được IH vuông góc MN (3)
Từ (1);(2) và (3) suy ra ba điểm I,H,K thẳng hàng. Đó là điều phải chứng minh.