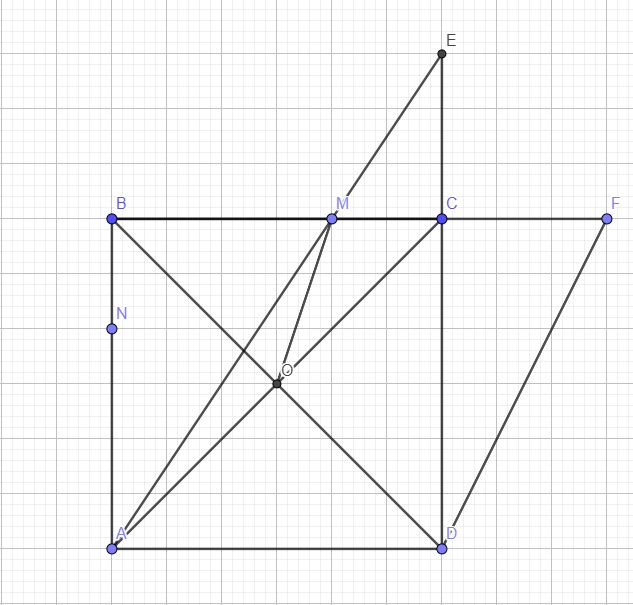
Cho hình chữ nhật ABCD.Trên tia đối của tia CD lấy điểm F sao cho CF=CB.Trên tia đối của tia CB lấy điểm E sao cho CD=CE.AE cắt CD tại M. AF cắt BC tại N. Chứng minh : DM=BN
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đặt cạnh hình vuông là a, ta có \(BD=\sqrt{a^2+a^2}=a\sqrt{2}\)
\(\Rightarrow BO=\dfrac{1}{2}BD=\dfrac{a\sqrt{2}}{2}\Rightarrow BO.BD=a^2\)
Xét 2 tam giác vuông AED và MAB có:
\(\left\{{}\begin{matrix}\widehat{ADE}=\widehat{MBA}=90^0\\\widehat{AED}=\widehat{MAB}\left(slt\right)\end{matrix}\right.\) \(\Rightarrow\Delta AED\sim\Delta MAB\left(g.g\right)\)
\(\Rightarrow\dfrac{AD}{BM}=\dfrac{ED}{AB}\Rightarrow BM.ED=AD.AB=a^2\)
\(\Rightarrow BM.ED=BO.BD\)
Mà \(ED=BF\) (do \(BC=CD\) và \(CE=CF\))
\(\Rightarrow BM.BF=BO.BD\Rightarrow\dfrac{BM}{BD}=\dfrac{BO}{BF}\)
Xét hai tam giác BOM và BFD có:
\(\left\{{}\begin{matrix}\dfrac{BM}{BD}=\dfrac{BO}{BF}\\\widehat{OBM}\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta BOM\sim\Delta BFD\left(c.g.c\right)\)

*Kẻ OI ⊥ EM, OH ⊥ FM. (1)
Theo đề, ta có AB=CD, AE=BM, CF=DM
Mà AI+EA=EI, IB+BM=IB và MD+DH=MH, HC+CF=HF
=>EM=MF (2)
Từ (1) và (2), suy ra:
IO=OH (định lí giữa dây và khoảng cách từ tâm đến dây)(3)
EI=IM, MH=HF(định lí đường kính và dây) => EI=IM=MH= HF (4)
Xét △EOI và △FOH, có:
EI=FH (theo (4)) , góc EIO= góc FHO (=90o)
IO=OH (theo(3))
=> △EIO=△FOH (c.g.c)
Do đó: OE=OF ( 2 cạnh tương ứng)
Vậy OE=OF (đpcm)
HAVE A GOOD DAY!