Biết rằng hàm số \(y=ax^2+bx+c\left(a\ne0\right)\) đạt giá trị lớn nhất bằng\(\frac{1}{4}\) tại \(x=\frac{3}{2}\) và tổng lập phương các nghiệm của phương trình y=0 bằng 9. Tính P = abc
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 11 2019
\(\left\{{}\begin{matrix}-\frac{b}{2a}=\frac{3}{2}\\\frac{4ac-b^2}{4a}=\frac{1}{4}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}b=-3a\\4ac-b^2=a\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}b=-3a\\4ac-9a^2=a\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}b=-3a\\4c-9a=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}b=-3a\\c=\frac{9a+1}{4}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1+x_2=-\frac{b}{a}=3\\x_1x_2=\frac{c}{a}=\frac{9a+1}{4a}\end{matrix}\right.\)
Ta có \(x_1^3+x_2^3=9\)
\(\Leftrightarrow\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)=9\)
\(\Leftrightarrow27-9\left(\frac{9a+1}{4a}\right)=9\)
\(\Rightarrow a=-1\Rightarrow\left\{{}\begin{matrix}b=3\\c=-2\end{matrix}\right.\) \(\Rightarrow P=6\)
XO
2 tháng 2 2022
c) Có \(P=\frac{ax+b}{x^2+1}=-1+\frac{x^2+ax+b+1}{x^2+1}\);
\(P=\frac{ax+b}{x^2+1}=4-\frac{4x^2-ax-b+4}{x^2+1}\)
Để Min P = 1 và Max P = 4 thì
\(\hept{\begin{cases}x^2+ax+b+1=\left(x+c\right)^2\\4x^2-ax-b+4=\left(2x+d\right)^2\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x\left(a-2c\right)+\left(b+1-c^2\right)=0\left(1\right)\\x\left(-a-4d\right)+\left(-b+4-d^2\right)=0\left(2\right)\end{cases}}\)
(1) = 0 khi \(\hept{\begin{cases}a=2c\\b=c^2-1\end{cases}}\)(3)
(2) = 0 khi \(\hept{\begin{cases}a=-4d\\b=4-d^2\end{cases}}\)(4)
Từ (3) (4) => d = 1 ; c = -2 ; b = 3 ; a = -4
Vậy \(P=\frac{-4x+3}{x^2+1}\)
XO
3 tháng 2 2022
ĐK \(x\ge y\)
Đặt \(\sqrt{x+y}=a;\sqrt{x-y}=b\left(a;b\ge0\right)\)
HPT <=> \(\hept{\begin{cases}a^4+b^4=82\\a-2b=1\end{cases}}\Leftrightarrow\hept{\begin{cases}\left(2b+1\right)^4+b^4=82\\a=2b+1\end{cases}}\Leftrightarrow\hept{\begin{cases}17b^4+32b^3+24b^2+8b-81=0\\a=2b+1\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}17b^4-17b^3+49^3-49b^2+73b^2-73b+81b-81=0\\a=2b+1\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}\left(b-1\right)\left(17b^3+49b^2+73b+81\right)=0\left(1\right)\\a=2b+1\end{cases}}\)
Giải (1) ; kết hợp điều kiện => b = 1
=> Hệ lúc đó trở thành \(\hept{\begin{cases}b=1\\a=2b+1\end{cases}}\Leftrightarrow\hept{\begin{cases}b=1\\a=3\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}\sqrt{x+y}=3\\\sqrt{x-y}=1\end{cases}}\Leftrightarrow\hept{\begin{cases}x+y=9\\x-y=1\end{cases}}\Leftrightarrow\hept{\begin{cases}2x=10\\x-y=1\end{cases}}\Leftrightarrow\hept{\begin{cases}x=5\\x-y=1\end{cases}}\Leftrightarrow\hept{\begin{cases}x=5\\y=4\end{cases}}\)
Vậy hệ có 1 nghiệm duy nhất (x;y) = (5;4)
CM
7 tháng 2 2017
Đáp án C
Từ giả thiết, ta có hệ:
− b 2 a = − 2 4 a − 2 b + c = 5 a + b + c = − 1 ⇔ a = − 2 3 ; b = − 8 3 ; c = 7 3
⇒ S = a 2 + b 2 + c 2 = 13
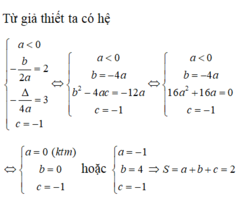
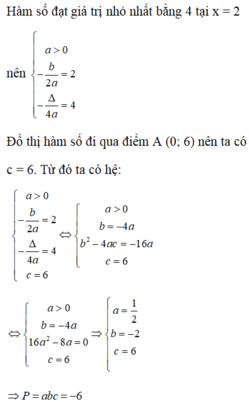
\(\left\{{}\begin{matrix}-\frac{b}{2a}=\frac{3}{2}\\\frac{4ac-b^2}{4a}=\frac{1}{4}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}b=-3a\\4ac-b^2=a\end{matrix}\right.\) \(\Rightarrow4ac-9a^2=a\Rightarrow c=\frac{9a+1}{4}\)
Mặt khác theo định lý Viet: \(\left\{{}\begin{matrix}x_1+x_2=-\frac{b}{a}=3\\x_1x_2=\frac{c}{a}=\frac{9a+1}{4a}\end{matrix}\right.\)
\(x_1^3+x_2^3=9\)
\(\Leftrightarrow\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)=9\)
\(\Leftrightarrow27-9\left(\frac{9a+1}{4a}\right)=9\)
\(\Leftrightarrow12a-9a-1=4a\Rightarrow a=-1\)
\(\Rightarrow b=3\) ; \(c=-2\)
\(P=6\)