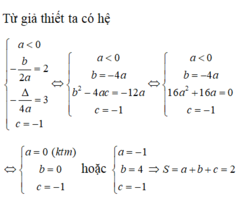Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\left\{{}\begin{matrix}-\frac{b}{2a}=\frac{3}{2}\\\frac{4ac-b^2}{4a}=\frac{1}{4}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}b=-3a\\4ac-b^2=a\end{matrix}\right.\) \(\Rightarrow4ac-9a^2=a\Rightarrow c=\frac{9a+1}{4}\)
Mặt khác theo định lý Viet: \(\left\{{}\begin{matrix}x_1+x_2=-\frac{b}{a}=3\\x_1x_2=\frac{c}{a}=\frac{9a+1}{4a}\end{matrix}\right.\)
\(x_1^3+x_2^3=9\)
\(\Leftrightarrow\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)=9\)
\(\Leftrightarrow27-9\left(\frac{9a+1}{4a}\right)=9\)
\(\Leftrightarrow12a-9a-1=4a\Rightarrow a=-1\)
\(\Rightarrow b=3\) ; \(c=-2\)
\(P=6\)

\(\left\{{}\begin{matrix}-\frac{b}{2a}=\frac{3}{2}\\\frac{4ac-b^2}{4a}=\frac{1}{4}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}b=-3a\\4ac-b^2=a\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}b=-3a\\4ac-9a^2=a\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}b=-3a\\4c-9a=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}b=-3a\\c=\frac{9a+1}{4}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1+x_2=-\frac{b}{a}=3\\x_1x_2=\frac{c}{a}=\frac{9a+1}{4a}\end{matrix}\right.\)
Ta có \(x_1^3+x_2^3=9\)
\(\Leftrightarrow\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)=9\)
\(\Leftrightarrow27-9\left(\frac{9a+1}{4a}\right)=9\)
\(\Rightarrow a=-1\Rightarrow\left\{{}\begin{matrix}b=3\\c=-2\end{matrix}\right.\) \(\Rightarrow P=6\)

Đáp án C
Từ giả thiết, ta có hệ:
− b 2 a = − 2 4 a − 2 b + c = 5 a + b + c = − 1 ⇔ a = − 2 3 ; b = − 8 3 ; c = 7 3
⇒ S = a 2 + b 2 + c 2 = 13