Chứng minh P là phân số tối giản: P = (2n3 +3n2 -n-1) / (2n3 +3n2 +3n +1)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


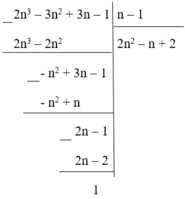
2 n 3 – 3 n 2 + 3n – 1 = (2 n 2 – n + 2)(n – 1) + 1
Để 2 n 3 – 3 n 2 + 3n – 1 chia hết cho n – 1 thì 1 chia hết cho n – 1
=> (n – 1) Є {1;-1}
n – 1 1 -1
n 2 0
P 9 1
TM TM
Vậy n Є {0; 2} để P Є Z
Đáp án cần chọn là: A

Ta có: u n = − 2 n 3 + 3 n 2 + 4 n 4 + 4 n 3 + n = − 2 n 3 + 3 n 2 + 4 n 4 n 4 + 4 n 3 + n n 4 = − 2 n + 3 n 2 + 4 n 4 1 + 4 n + 1 n 3
Mà lim 2 n = 0 , lim 3 n 2 = 0 , lim 4 n 4 = 0 , lim 4 n = 0 v à lim 1 n 3 = 0
Do đó lim u n = 0 + 0 + 0 1 + 0 + 0 = 0
Chọn đáp án B

lim 2 n 4 − 3 n 3 + 2 n 3 + 2 = lim n 4 2 − 3 n + 2 n 4 n 3 1 + 2 n 3 = lim n . 2 − 3 n + 2 n 4 1 + 2 n 3 = + ∞
Vì lim n = + ∞ ; lim 2 − 3 n + 2 n 4 1 + 2 n 3 = 2

Chia cả tử và mẫu của phân thức cho n 3 ( n 3 là lũy thừa bậc cao nhất của n trong phân thức), ta được:
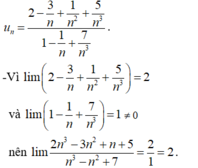
Chọn C.

Đáp án C
Chia cả tử và mẫu của phân thức cho n3 ( n3 là lũy thừa bậc cao nhất củan trong phân thức), ta được:
u n = 2 n 3 - 3 n 2 + n + 5 n 3 - n 2 + 7 = 2 - 3 n + 1 n 2 + 5 n 3 1 - 1 n + 7 n 3 .
Vì l i m 2 - 3 n + 1 n 2 + 5 n 3 = 2 và l i m 1 - 1 n + 7 n 3 = 1 ≢ 0 nên l i m 2 n 3 - 3 n 2 + n + 5 n 3 - n 2 + 7 = 2 1 = 2 .

\(lim\dfrac{6n^3-2n+3}{2n^3-3n^2-5n+1}=lim\dfrac{6-\dfrac{2}{n^2}+\dfrac{3}{n^3}}{2-\dfrac{3}{n}-\dfrac{5}{n^2}+\dfrac{1}{n^3}}=\dfrac{6-0+0}{2-0-0+0}=3\)

Gọi d=ƯCLN(3n,3n+1) Suy ra 3n chia hết cho d và 3n+1 chia hết cho d Suy ra (3n+1)-3nchia hết cho d Suy ra 3n+1-3n chia hết cho d Suy ra 1chia hết cho d,suy ra d=1,suy ra ƯCLN(3n,3n+1)=1 Suy ra 3n/3n+1 là ps tối giản Chứng tỏ 3n/3n+1(n thuộc N) là phân số tối giản
zì hai số tự nhiên liên tiếp nhau khác 0 sẽ ko cùng chia hết cho số nào lớn hơn1
tử số là số bé mà mẫu số là số lớn hơn số bé 1 đơn vị
điều này chứng tỏ hai số này là hay số tự nhiên liên tiếp
=> nó là phân số tối giản
vì 3n và 3n+1 là hai số tự nhiên liên tiếp

Gọi UCLN của 2 số đó là d
2-3n chia hết cho d
3n-1 chia hết cho d
2-3n+3n-1 chia hết chod
1 chia hết cho d
d=1
2-3n/3n-1 tối giản
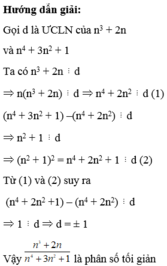
\(P=\frac{\left(2n^3+n^2\right)+\left(2n^2+n\right)-\left(2n+1\right)}{\left(2n^3+n^2\right)+\left(2n^2+n\right)+\left(2n+1\right)}\)
\(P=\frac{n^2\left(2n+1\right)+n\left(2n+1\right)-\left(2n+1\right)}{n^2\left(2n+1\right)+n\left(2n+1\right)+\left(2n+1\right)}\)
\(P=\frac{n^2\left(2n+1\right)+n\left(2n+1\right)-\left(2n+1\right)}{n^2\left(2n+1\right)+n\left(2n+1\right)+\left(2n+1\right)}\)
P không là tối giản vì cả tử và mẫu đều chia hết cho (2n +1)
ban thieu DKXD:N=/\(\frac{-1}{2}\)