(2 -x)(x+2/3)>0 tìm x
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a:
Sửa đề: \(P=\left(\dfrac{3+x}{3-x}-\dfrac{3-x}{3+x}-\dfrac{4x^2}{x^2-9}\right):\left(\dfrac{5}{3-x}-\dfrac{4x+2}{3x-x^2}\right)\)\(P=\left(\dfrac{-\left(x+3\right)}{x-3}+\dfrac{x-3}{x+3}-\dfrac{4x^2}{\left(x-3\right)\left(x+3\right)}\right):\dfrac{5x-4x-2}{x\left(3-x\right)}\)
\(=\dfrac{-x^2-6x-9+x^2-6x+9-4x^2}{\left(x-3\right)\left(x+3\right)}:\dfrac{x-2}{x\left(3-x\right)}\)
\(=\dfrac{-4x^2-12x}{\left(x-3\right)\left(x+3\right)}\cdot\dfrac{x\left(3-x\right)}{x-2}\)
\(=\dfrac{-4x\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}\cdot\dfrac{-x\left(x-3\right)}{x-2}=\dfrac{4x^2}{x-2}\)
b: x^2-4x+3=0
=>x=1(nhận) hoặc x=3(loại)
Khi x=1 thì \(P=\dfrac{4\cdot1^2}{1-2}=-4\)
c: P>0
=>x-2>0
=>x>2
d: P nguyên
=>4x^2 chia hết cho x-2
=>4x^2-16+16 chia hết cho x-2
=>x-2 thuộc {1;-1;2;-2;4;-4;8;-8;16;-16}
=>x thuộc {1;4;6;-2;10;-6;18;-14}

b) 5x(x-2000)-x+2000=0
\(\Rightarrow5x\left(x-2000\right)-\left(x-2000\right)=0\\ \Rightarrow\left(x-2000\right)\left(5x-1\right)=0\)
\(\Rightarrow\left\{{}\begin{matrix}x-2000=0\\5x-1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0+2000\\5x=0+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2000\\5x=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2000\\x=\dfrac{1}{5}\end{matrix}\right.\)

b) \(x^3-x^2-x+1=0\Leftrightarrow\left(x-1\right)^2\left(x+1\right)=0\)
\(\Leftrightarrow x-1=0\) hoặc \(x+1=0\)
\(\Leftrightarrow x=1\) hoặc \(x=-1\)
c) \(x^2-6x+8=0\Leftrightarrow\left(x-4\right)\left(x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-4=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\\x=2\end{matrix}\right.\)
a) \(x^3+x^2+x+1=0\Leftrightarrow\left(x+1\right)\left(x^2+1\right)=0\Leftrightarrow x+1=0\Leftrightarrow x=-1\)
(do \(x^2+1\ge1>0\))

a) (x - 3)2 - 5.(x - 2) + 5 = 0.
<=> x^2 - 6x + 9 - 5x + 10 + 5 = 0
<=> x^2 - 11x + 24 = 0
<=> (x-3)(x-8)=0
<=> x = 3 hoặc x = 8

d: Ta có: \(9x^2+6x-8=0\)
\(\Leftrightarrow9x^2+12x-6x-8=0\)
\(\Leftrightarrow\left(3x+4\right)\left(3x-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{4}{3}\\x=\dfrac{2}{3}\end{matrix}\right.\)
e: Ta có: \(x\left(x-2\right)+x-2=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)
f: Ta có: \(5x\left(x-3\right)-x+3=0\)
\(\Leftrightarrow\left(x-3\right)\left(5x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=\dfrac{1}{5}\end{matrix}\right.\)

( 2x - 3 )( x + 1 ) - 2x2 + 6x = 0
<=> 2x2 - x - 3 - 2x2 + 6x = 0
<=> 5x - 3 = 0
<=> 5x = 3
<=> x = 3/5
( x2 - x + 1 )( x - 3 ) - x3 + 4x2 = 0
<=> x3 - 4x2 + 4x - 3 - x3 + 4x2 = 0
<=> 4x - 3 = 0
<=> 4x = 3
<=> x = 3/4
( x2 - 2 )( x2 + 2 ) - x4 - 2x + 5 = 0
<=> ( x2 )2 - 4 - x4 - 2x + 5 = 0
<=> x4 + 1 - x4 - 2x = 0
<=> 1 - 2x = 0
<=> 2x = 1
<=> x = 1/2
( x - 3 )( x2 - 3x + 2 ) - ( x2 - 2x - 7 )( x - 2 ) + 2x2 - 2x = 0
<=> x3 - 6x2 + 11x - 6 - ( x3 - 4x2 - 3x + 14 ) + 2x2 - 2x = 0
<=> x3 - 6x2 + 11x - 6 - x3 + 4x2 + 3x - 14 + 2x2 - 2x = 0
<=> 12x - 20 = 0
<=> 12x = 20
<=> x = 20/12 = 5/3
a, \(\left(2x-3\right)\left(x+1\right)-2x^2+6x=0\)
\(\Leftrightarrow2x^2+2x-3x-3-2x^2+6x=0\Leftrightarrow5x-3=0\Leftrightarrow x=\frac{3}{5}\)
b, \(\left(x^2-x+1\right)\left(x-3\right)-x^3+4x^2=0\)
\(\Leftrightarrow x^3-3x^2-x^2+3x+x-3-x^3+4x^2=0\Leftrightarrow4x-3=0\Leftrightarrow x=\frac{3}{4}\)
c ; d tương tự nhé !

1/ ( x+12)(3-x)=0
=> \(\orbr{\begin{cases}x+12=0\\3-x=0\end{cases}}\)
=>\(\orbr{\begin{cases}x=-12\\x=3\end{cases}}\)
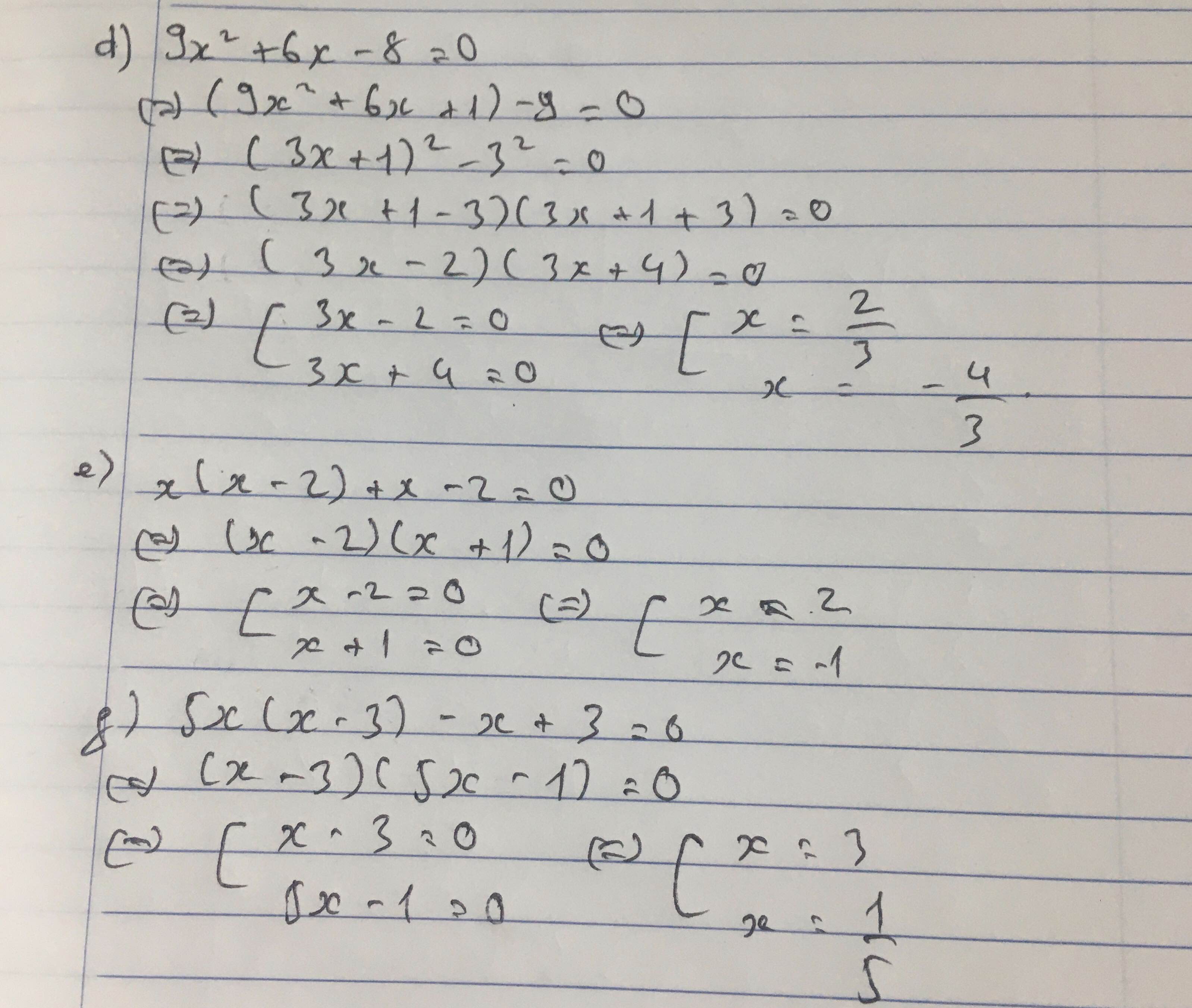 Mình trình bày trong hình ^^ Bn tham khảo nhé
Mình trình bày trong hình ^^ Bn tham khảo nhé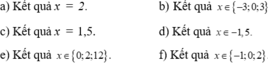
\(\left(2-x\right)\left(x+\frac{2}{3}\right)>0\)
th1 :
\(\hept{\begin{cases}2-x>0\\x+\frac{2}{3}>0\end{cases}\Rightarrow\hept{\begin{cases}x< 2\\x< -\frac{2}{3}\end{cases}\Rightarrow}x< -\frac{2}{3}}\)
th2 :
\(\hept{\begin{cases}2-x< 0\\x+\frac{2}{3}< 0\end{cases}}\Rightarrow\hept{\begin{cases}x>2\\x< -\frac{2}{3}\end{cases}\Rightarrow loai}\)