Mọi người viết các đa thức thành tích cho mình với
K
Khách
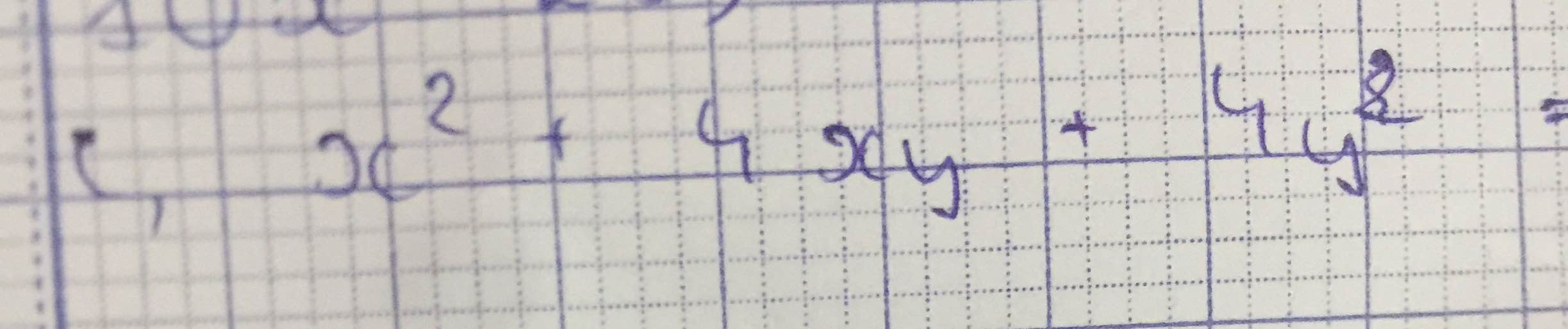
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 11 2021
\(64-x^2-y^2+2xy=64-\left(x^2-2xy+y^2\right)\)
\(=8^2-\left(x-y\right)^2=\left(8-x+y\right)\left(8+x-y\right)\)
VF
1
30 tháng 9 2017
Ta có: \(6x^2-7x+2=6x^2-3x-4x+2\)
\(=\left(6x^2-3x\right)-\left(4x-2\right)\)
\(=3x\left(2x-1\right)-2\left(2x-1\right)\)
\(=\left(2x-1\right)\left(3x-2\right)\)
LT
1
VF
0
27 tháng 10 2023
Để phân tích đa thức thành nhân tử, ta có thể sử dụng phương pháp phân tích hệ số hoặc sử dụng định lý nhân tử của đa thức. Trong trường hợp này, chúng ta sẽ sử dụng phương pháp phân tích hệ số.
Đa thức: x^4 - 2x^3 + 10x^2 + 9x + 14
Đầu tiên, chúng ta sẽ tìm các ước của hệ số tự do (14). Các ước của 14 là ±1, ±2, ±7 và ±14. Tiếp theo, chúng ta sẽ thử từng ước này vào đa thức để kiểm tra xem có tồn tại nhân tử nào cho đa thức hay không.
Thử với ước 1: 1^4 - 2(1)^3 + 10(1)^2 + 9(1) + 14 = 32
Thử với ước -1: (-1)^4 - 2(-1)^3 + 10(-1)^2 + 9(-1) + 14 = 16
Thử với ước 2: 2^4 - 2(2)^3 + 10(2)^2 + 9(2) + 14 = 58
Thử với ước -2: (-2)^4 - 2(-2)^3 + 10(-2)^2 + 9(-2) + 14 = 10
Thử với ước 7: 7^4 - 2(7)^3 + 10(7)^2 + 9(7) + 14 = 2064
Thử với ước -7: (-7)^4 - 2(-7)^3 + 10(-7)^2 + 9(-7) + 14 = 1288
Thử với ước 14: 14^4 - 2(14)^3 + 10(14)^2 + 9(14) + 14 = 25088
Thử với ước -14: (-14)^4 - 2(-14)^3 + 10(-14)^2 + 9(-14) + 14 = 20096
Dựa vào kết quả trên, ta thấy rằng không có ước nào cho đa thức. Do đó, ta kết luận rằng đa thức x^4 - 2x^3 + 10x^2 + 9x + 14 không thể phân tích thành nhân tử trong trường số thực.
b: \(x^2+10x+25=\left(x+5\right)^2\)
c: \(x^2+4xy+4y^2=\left(x+2y\right)^2\)