Cho tam giác ABC đều, cạnh là 6cm. Tính độ dài đường cao.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Hình bạn tự vẽ nhá :v
Vì tam giác ABC là tam giác đều
=> AI vừa là đường cao , vừa là đường trung tuyến ứng với BC
=> I là trung điểm BC
=> IC = 6:2 = 3 cm
Xét tam giác AIC vuông tại I
Áp dụng định lí Pitago , ta có :
AI2 = IC2 + AC2
=> AI2 = 32 + 62 = 9+36 = 45
=> AI = √45 ( vì độ dài AI luôn dương)

Câu 1:
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
\(\Leftrightarrow\dfrac{1}{AH^2}=\dfrac{1}{9^2}+\dfrac{1}{12^2}=\dfrac{1}{81}+\dfrac{1}{144}=\dfrac{25}{1296}\)
\(\Leftrightarrow AH^2=\dfrac{1296}{25}\)
hay \(AH=\dfrac{14}{5}=4.8cm\)
Vậy: AH=4,8cm
Câu 2:
Ta có: BC=BH+CH(H nằm giữa B và C)
hay BC=5+6=11(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AB^2=BH\cdot BC\)
\(\Leftrightarrow AB^2=5\cdot11=55\)
hay \(AB=\sqrt{55}cm\)
Vậy: \(AB=\sqrt{55}cm\)
Câu 4:
Không có hàm số nào không phải là hàm số bậc nhất

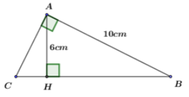
Áp dụng định lý Pytago trong tam giác ABH vuông tại H. Ta có:
![]()
Trong tam giác vuông ABC vuông tại A có AH là đường cao
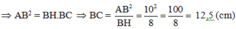
Áp dụng định lý Py-ta-go cho tam giác vuông ABC ta có:
![]()
Vậy AC = 7,5 (cm); BC = 12,5 (cm)
Đáp án cần chọn là: B

TL LAỊ NHÉ
\(\sqrt{6^2-3^2}=3\sqrt{3}\)
HT Ạ
@@@@@@@@@
ta thấy tam giác đều sẽ có đường cao đồng thời là đừng trung tuyến(tam giác đều cũng là tam giác cân)
nên khi ta kẻ đừơng cao của tam giác đều,sẽ cia ta giác đều đó thành hai tam giác vuông có độ dài cạnh huyền là 6 cm và độ dài 1 cạnh góc vuông là 3cm.cạnh còn lại chính là đừng cao của tam giác đều đó
theo định lí pytago,ta sẽ tinhs đc độ dài đừng cao đó sẽ là
\(\sqrt{6^2-3^2}\)=5(cm)(do độ dài cạnh tam giác lớn hơn 0)
HT Ạ

dựa vào công thức diện tích nên ah x bc = bk x ac
>> 5 x bc = 6 x (22-bc) = 132 - 6 x bc
>> 132 - 11 x bc = 0 >> bc = 12 >> ac = 10

Câu 1:
a: AH=3x4:5=2,4(cm)
b: HC=16:5=3,2(cm)
Xét ΔAHC vuông tại H có
\(\sin HAC=\dfrac{HC}{AC}=\dfrac{3.2}{4}=\dfrac{4}{5}\)
nên \(\widehat{HAC}=53^0\)
Vẽ đường cao AH
Xét tam giác AHB và tam giác AHC có :
AHB=AHC=90
HAB = HAC=30
AH chung
nên tam gíac AHB = tam giác AHC(cạnh góc vuông góc nhọn kề)
=>HB=HC(2 cạnh tương ứng)
=>HB=1/2BC=1/2 . 6=3 cm
Áp dụng đl ptg vào là ra
Mik ko dùng đường trung tuyến vì nó ở HK2 lớp 7 nha