Cho xy # 0 và x+y=1. Chứng minh rằng :
\(\frac{x}{y^3-1}\)+ \(\frac{y}{x^3-1}\)- \(\frac{2\left(xy-2\right)}{x^2y^2+3}\)= 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

`a, (x-y)^2 = (x+y)^2 - 4xy = 12^2 - 35 . 4 = 144 - 140 = 4`.
`b, (x+y)^2 = (x-y)^2 + 4xy = 8^2 + 20.4 = 64 + 80 = 144`
`c, x^3 + y^3 = (x+y)^3 - 3xy(x+y) = 5^3 - 3 . 6 . 5 = 125 - 90 = 35`
`d, x^3 - y^3 = (x-y)^3 - 3xy(x-y) = 3^3 - 3 .40 . 3 = 27 - 360 = -333`.

AB cắt xy và BC cắt xy nên A và C cùng thuộc nửa mặt phẳng bờ xy
BC cắt xy và CD cắt xy nên B và D cùng thuộc nửa mặt phằng bờ xy không chứa A,C => BD ko cắt xy
A,D ko cùng nửa mặt phẳng bờ xy nên AD cắt xy

Vẽ đoạn thẳng MN cắt xy tại C
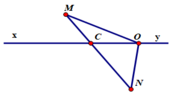
Lấy điểm O thuộc tia Cy thì tia Ox nằm giữa hai tia OM, ON

\(6xy=x+y\ge2\sqrt[]{xy}\Rightarrow\sqrt{xy}\ge\dfrac{1}{3}\Rightarrow xy\ge\dfrac{1}{9}\Rightarrow\dfrac{1}{xy}\le9\)
\(M=\dfrac{\dfrac{x+1}{xy+1}+\dfrac{xy+x}{1-xy}+1}{1+\dfrac{xy+x}{1-xy}-\dfrac{x+1}{xy+1}}=\dfrac{\dfrac{x+1}{xy+1}+\dfrac{x+1}{1-xy}}{\dfrac{x+1}{1-xy}-\dfrac{x+1}{xy+1}}=\dfrac{\dfrac{1}{1-xy}+\dfrac{1}{1+xy}}{\dfrac{1}{1-xy}-\dfrac{1}{1+xy}}\)
\(M=\dfrac{1+xy+1-xy}{1+xy-1+xy}=\dfrac{2}{2xy}=\dfrac{1}{xy}\le9\)
Dấu "=" xảy ra khi \(x=y=\dfrac{1}{3}\)

Bạn kham khảo câu này nhé dù không làm nhưng bạn có thể cho mình 1 tk được ko.
Câu hỏi của Trịnh Tuấn Tú - Toán lớp 7 - Học toán với OnlineMath

Vẽ đoạn thẳng MN cắt xy tại C
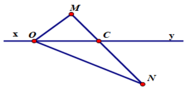
Lấy điểm O thuộc tia Cx, O khác C thì tia Ox không nằm giữa OM, ON.