Bài Toán:Cho tam giác ABC vuông tại A.Gọi M là trung điểm của cạnh AC; trên tia đối tia MB lấy điểm E sao cho ME=MB
a) Cm: tam giác AMB = tam giác CME
b) So sánh CE và BC
c) So sánh góc ABM và góc MBC
d) Cm: AE // BC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Tam giác \(ABC\) cân tại \(A\)
\(\Rightarrow AB=AC;\widehat{B}=\widehat{C}\)
Xét \(\Delta ABM;\Delta ACM\) có
\(AB=AC\left(cmt\right)\\ \widehat{B}=\widehat{C}\left(cmt\right)\\ MB=MC\)
\(\Rightarrow\Delta ABM=\Delta ACM\left(c-g-c\right)\)
b, \(\Delta ABM=\Delta ACM\left(cmt\right)\)
\(\Rightarrow\widehat{HAM}=\widehat{KAM}\)
Xét \(\Delta AHM;\Delta AKM\) có
\(\widehat{HAM}=\widehat{KAM}\left(cmt\right)\\ \widehat{AHM}=\widehat{AKM}=90^o\)
\(AM\) chung
\(\Rightarrow\Delta AHM=\Delta AKM\left(ch-gn\right)\)
\(\Rightarrow HM=KM\)

a) Xét tam giác ABC vuông tại A có:
+ E là trung điểm của AB (gt).
+ F là trung điểm của AC (gt).
=> EF là đường trung bình (định nghĩa đường trung bình trong tam giác).
=> 2EF = BC (Tính chất đường trung bình trong tam giác).
=> 2.4 = 8 (cm).
b) Xét tứ giác AECM có:
+ F là trung điểm của EM (do M là điểm đối xứng của E qua F).
+ F là trung điểm của AC (gt).
=> Tứ giác AECM là hình bình (dhnb).

a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó: ΔABM=ΔACM
Ta có: ΔBAC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
b: Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
\(\widehat{EAM}=\widehat{FAM}\)
Do đó; ΔAEM=ΔAFM
Suy ra: ME=MF
hay ΔMEF cân tại M
c: BC=6cm nên BM=CM=3cm
=>AM=4cm
d: Xét ΔABC có AE/AB=AF/AC
nên EF//BC

\(\text{#TNam}\)
`a,` Vì Tam giác `ABC` cân tại `A -> AB = AC,`\(\widehat{B}=\widehat{C}\)
Xét Tam giác `AIB` và Tam giác `AIC` có:
`AB = AC (CMT)`
\(\widehat{B}=\widehat{C}\) `(CMT)`
`IB = IC (g``t)`
`=> \text {Tam giác AIB = Tam giác AIC (c-g-c)}`
Hnhu câu `b,` bạn ghi thiếu yêu cầu rồi nhé!
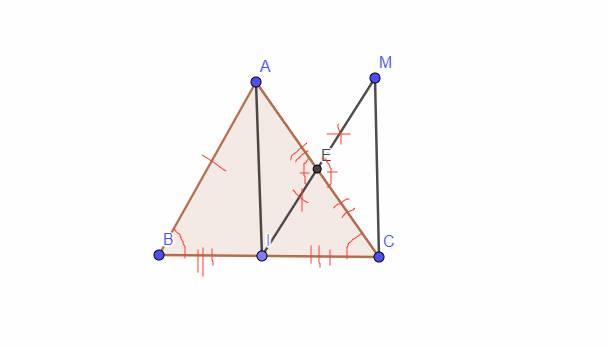
`c,` Xét Tam giác `AEI` và Tam giác `MEC` có:
`EA = EC (g``t)`
\(\widehat{AEI}=\widehat{MEC}\) `(\text {2 góc đối đỉnh})`
`EM = EI (g``t)`
`=> \text {Tam giác AEI = Tam giác MEC (c-g-c)}`
`->`\(\widehat{AIE}=\widehat{CME}\) `(\text {2 góc tương ứng})`
Mà `2` góc này nằm ở vị trí sole trong `-> \text {AI // CM}`
Vì Tam giác `ABI =` Tam giác `ACI (a)`
`->`\(\widehat{AIB}=\widehat{AIC}\) `(\text {2 góc tương ứng})`
Mà `2` góc này nằm ở vị trí kề bù
`->`\(\widehat{AIB}+\widehat{AIC}=180^0\)
`->`\(\widehat{AIB}=\widehat{AIC}=\) `180/2=90^0`
`-> AI \bot BC`
Mà `\text {AI // CM} -> MC \bot BC`

c.theo chứng minh câu b là tam giác BMH =tam giác KMC nên ta có góc BMH= góc CMK
vì MK vuông góc với AC và BP vuông góc với AC nên BP//MK(từ vuong góc tới//)
nên => góc PMC = góc KMC(đồng vị)
vậy ta có góc PBC= góc BMH( vì cùng bằng góc KMC)
nên tam giác BIM cân tại I
a) Vì tam giác ABC là tam giác cân có
AM là đường trugn tuyến
nên AM vừa là đường cao vừa là đường phân giác
=> Góc BAM = góc MAC
Xét \(\Delta AMB\) và \(\Delta MAC\)CÓ
góc BAM = góc CAM ( CMT)
AM chung
AMB = góc AMC ( cùng bằng 90 độ )
Vậy Tam giác ABM = tam giác AMC ( c-g-v-g-n-k)
b) Xét tam giác AHM và tam giác AKM có
AM chung
Góc AHM =AKM ( = 90 độ)
HAM =MAK ( cmt câu a)
nên Tam giác AHM = tam giác AKM (c-h-g-n)
=> HM = MK
và BHM = MKC , góc B= C
Nên tam giác BHM = KMC
=> HB = KC
c) Ta có BP VUÔNG GÓC VỚI AC
và MK vuông góc với AC
Nên BP// MK
=> góc PBM = KMC
Mà KMC = HMB ( vÌ tam giác BHM = KMC )
Suy ra : PBM = góc HMB
Hay tam giác IBM cân tại I
Cm: a) Xét t/giác AMB và t/giác CME
có: AM = MC (gt)
BM = ME (gt)
\(\widehat{AMB}=\widehat{CME}\)(đối đỉnh)
=> t/giác AMB = t/giác CME (c.g.c)
b) Ta có: AB < BC (cgv < ch)
Mà AB = CE (vì t/giác AMB = t/giác CME)
=> CE < BC
c) Ta có: CE < BC (cmt)
=> \(\widehat{MBC}< \widehat{MEC}\) (quan hệ giữa góc và cạnh đối diện)
Mà \(\widehat{MEC}=\widehat{ABM}\) (vì t/giác AMB = t/giác CME)
=> \(\widehat{ABM}>\widehat{MBC}\)
d) Xét t/giác AME và t/giác CMB
có: AM = MC (gt)
ME = MB (gt)
\(\widehat{AME}=\widehat{CMB}\)(đối đỉnh)
=> t/giác AME = t/giác CMB (c.g.c)
=> \(\widehat{CBM}=\widehat{MEA}\) (2 góc t/ứng)
Mà 2 góc này ở vị trí so le trong
=> AE // BC (Đpcm)