Khảo sat sự biến thiên của hàm số: y=\(\sqrt{x-4}\) + \(\sqrt{x+1}\) trên khoảng (4;\(+\infty\))
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan
HN
0

LN
0


NM
26 tháng 1 2016
+TXĐ: X\(\in\)R
+y'=\(3x^2-6x\Rightarrow y'=0\Leftrightarrow\int_{x=2;y=0}^{x=0;y=4}\)
+y''=6(x-1)=> y' = 0 khi x = 1;y=2
+
| x | -\(\infty\) 0 1 2 +\(\infty\) |
| y' | + 0 - - 0 + |
| y |
LN
1

24 tháng 10 2021
TXĐ: D=[0;+\(\infty\))
Hàm số này luôn đồng biến với mọi x thuộc D
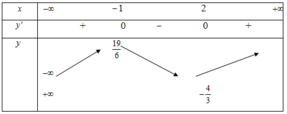


Với hai số thực bất kì \(4< a< b\) ta có:
\(y\left(b\right)-y\left(a\right)=\sqrt{b-4}-\sqrt{a-4}+\sqrt{b+1}-\sqrt{a+1}\)
\(=\frac{b-a}{\sqrt{b-4}+\sqrt{a-4}}+\frac{b-a}{\sqrt{b+1}+\sqrt{a+1}}=\left(b-a\right)\left(\frac{1}{\sqrt{b-4}+\sqrt{a-4}}+\frac{1}{\sqrt{b+1}+\sqrt{a+1}}\right)\)
\(\left\{{}\begin{matrix}b>a\Rightarrow b-a>0\\\frac{1}{\sqrt{b-4}+\sqrt{a-4}}+\frac{1}{\sqrt{b+1}+\sqrt{a+1}}>0\end{matrix}\right.\)
\(\Rightarrow y\left(b\right)-y\left(a\right)>0\) \(\forall b>a\)
\(\Rightarrow y\) đồng biến trên miền đã cho