Tìm tập gtln gtnn của hàm số y= 2sin^x + cos^22x
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 5 2019
\(y=2\left(\frac{1}{2}-\frac{1}{2}cos2x\right)+cos^22x=cos^22x-cos2x+1\)
\(=\left(cos2x-\frac{1}{2}\right)^2+\frac{3}{4}\ge\frac{3}{4}\)
\(\Rightarrow y_{min}=\frac{3}{4}\) khi \(cos2x=\frac{1}{2}\)
\(y=cos^22x-2cos2x+cos2x-2+3\)
\(y=\left(cos2x-2\right)\left(cos2x+1\right)+3\)
Do \(-1\le cos2x\le1\Rightarrow\left\{{}\begin{matrix}cos2x-2< 0\\cos2x+1\ge0\end{matrix}\right.\) \(\Rightarrow\left(cos2x-2\right)\left(cos2x+1\right)\le0\)
\(\Rightarrow y\le3\Rightarrow y_{max}=3\) khi \(cos2x=-1\)
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 7 2021
\(y=1-cos2x+2sin2x+6=2sin2x-cos2x+7\)
\(y=\sqrt{5}\left(\dfrac{2}{\sqrt{5}}sin2x-\dfrac{1}{\sqrt{5}}cos2x\right)+7\)
Đặt \(\dfrac{2}{\sqrt{5}}=cosa\) với \(a\in\left(0;\dfrac{\pi}{2}\right)\)
\(y=\sqrt{5}sin\left(2x-a\right)+7\)
\(\Rightarrow-\sqrt{5}+7\le y\le\sqrt{5}+7\)
21 tháng 7 2023
y=(sin2x-3)^2-6
-1<=sin2x<=1
=>-4<=sin2x-3<=-2
=>4<=(sin2x-3)^2<=16
=>-2<=y<=10
y min khi sin2x-3=-2
=>sin 2x=1
=>2x=pi/2+k2pi
=>x=pi/4+kpi
y max khi sin 2x-3=-4
=>sin 2x=-1
=>2x=-pi/2+k2pi
=>x=-pi/4+kpi
11 tháng 12 2023
1: \(y=x+\dfrac{4}{\left(x-2\right)^2}\)
\(\Leftrightarrow y'=1+\left(\dfrac{4}{\left(x-2\right)^2}\right)'\)
=>\(y'=1+\dfrac{4'\left(x-2\right)^2-4\left[\left(x-2\right)^2\right]'}{\left(x-2\right)^4}\)
=>\(y'=1+\dfrac{-4\cdot2\cdot\left(x-2\right)'\left(x-2\right)}{\left(x-2\right)^4}\)
=>\(y'=1-\dfrac{8}{\left(x-2\right)^3}\)
Đặt y'=0
=>\(\dfrac{8}{\left(x-2\right)^3}=1\)
=>\(\left(x-2\right)^3=8\)
=>x-2=2
=>x=4
Đặt \(f\left(x\right)=x+\dfrac{4}{\left(x-2\right)^2}\)
\(f\left(4\right)=4+\dfrac{4}{\left(4-2\right)^2}=4+1=5\)
\(f\left(0\right)=0+\dfrac{4}{\left(0-2\right)^2}=0+\dfrac{4}{4}=1\)
\(f\left(5\right)=5+\dfrac{4}{\left(5-2\right)^2}=5+\dfrac{4}{9}=\dfrac{49}{9}\)
Vì f(0)<f(4)<f(5)
nên \(f\left(x\right)_{max\left[0;5\right]\backslash\left\{2\right\}}=f\left(5\right)=\dfrac{49}{9}\) và \(f\left(x\right)_{min\left[0;5\right]\backslash\left\{2\right\}}=1\)
2: \(y=cos^22x-sinx\cdot cosx+4\)
\(=1-sin^22x-\dfrac{1}{2}\cdot sin2x+4\)
\(=-sin^22x-\dfrac{1}{2}\cdot sin2x+5\)
\(=-\left(sin^22x+\dfrac{1}{2}\cdot sin2x-5\right)\)
\(=-\left(sin^22x+2\cdot sin2x\cdot\dfrac{1}{4}+\dfrac{1}{16}-\dfrac{81}{16}\right)\)
\(=-\left(sin2x+\dfrac{1}{4}\right)^2+\dfrac{81}{16}\)
\(-1< =sin2x< =1\)
=>\(-\dfrac{3}{4}< =sin2x+\dfrac{1}{4}< =\dfrac{5}{4}\)
=>\(0< =\left(sin2x+\dfrac{1}{4}\right)^2< =\dfrac{25}{16}\)
=>\(0>=-\left(sin2x+\dfrac{1}{4}\right)^2>=-\dfrac{25}{16}\)
=>\(\dfrac{81}{16}>=-sin\left(2x+\dfrac{1}{4}\right)^2+\dfrac{81}{16}>=-\dfrac{25}{16}+\dfrac{81}{16}=\dfrac{7}{2}\)
=>\(\dfrac{81}{16}>=y>=\dfrac{7}{2}\)
\(y_{min}=\dfrac{7}{2}\) khi \(sin2x+\dfrac{1}{4}=\dfrac{5}{4}\)
=>\(sin2x=1\)
=>\(2x=\dfrac{\Omega}{2}+k2\Omega\)
=>\(x=\dfrac{\Omega}{4}+k\Omega\)
\(y_{max}=\dfrac{81}{16}\) khi sin 2x=-1
=>\(2x=-\dfrac{\Omega}{2}+k2\Omega\)
=>\(x=-\dfrac{\Omega}{4}+k\Omega\)
NM
1
30 tháng 9 2015
ta có \(y=2sin^4x+\left(1-2sin^2x\right)^2\)=\(2sin^4x+4sin^4x-4sinx^2+1=6sin^4x-4sin^2x+1\)
đặt \(t=sin^2x,0\le t\le1\)
ta đc \(y=6t^2-4t+1\)
ta tính y'=12t-4
giải pt y'=0 suy ra t=1/3
ta có bảng biến thiên
từ bảng bt ta suy ra hàm số đạt giá trị nhỏ nhất \(y=\frac{1}{3}\) khi \(t=\frac{1}{3}\Rightarrow sin^2x=\frac{1}{3}\)
hàm số đạt giá trị lớn nhất y=3 khi \(t=1\Rightarrow sin^2x=1\)
BN
0
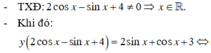
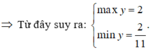
Đề là \(y=2sin^2x+cos^22x\) hả bạn? Và tìm GTNN, GTLN hay tìm tập giá trị?