Cho hàm số y=f( x) xác định và có đạo hàm trên R
(f(1+2x))^2=x- (f(1-2x))^3
Tính f'(1)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 8 2021
\(f'\left(x\right)=0\Rightarrow\left[{}\begin{matrix}x=-2\\x=3\end{matrix}\right.\) (chỉ quan tâm nghiệm bội lẻ)
\(g\left(x\right)=f\left(x^2-2x\right)\)
\(g'\left(x\right)=2\left(x-1\right)f'\left(x^2-2x\right)=0\Rightarrow\left[{}\begin{matrix}x=1\\f'\left(x^2-2x\right)=0\end{matrix}\right.\)
\(f'\left(x^2-2x\right)=0\Rightarrow\left[{}\begin{matrix}x^2-2x=-2\\x^2-2x=3\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-1\\x=3\end{matrix}\right.\)
BBT:
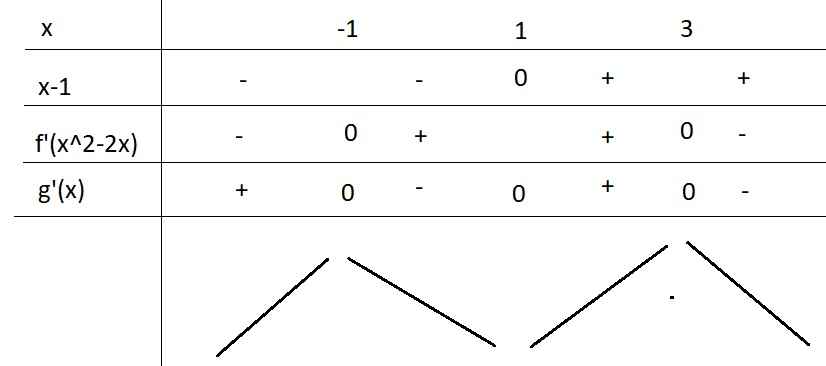
Từ BBT ta thấy \(f\left(x^2-2x\right)\) có 1 cực tiểu
CM
28 tháng 11 2019
Đáp án D
f ' ( x ) = 0 ⇔ ( x - 1 ) 2017 ( x 2 - 1 ) ( 2 x + 3 ) 3 = 0 ⇔ x = 1 x = - 1 x = - 3 2
Xét dấu:
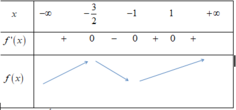
Vậy hàm số có 2 cực trị
và f(1) = -1. Khẳng định nào sau đây đúng?
có 
nghiệm trên 
.
có 1 nghiệm trên 
.
CM
17 tháng 2 2017
Đáp án A
, 
.
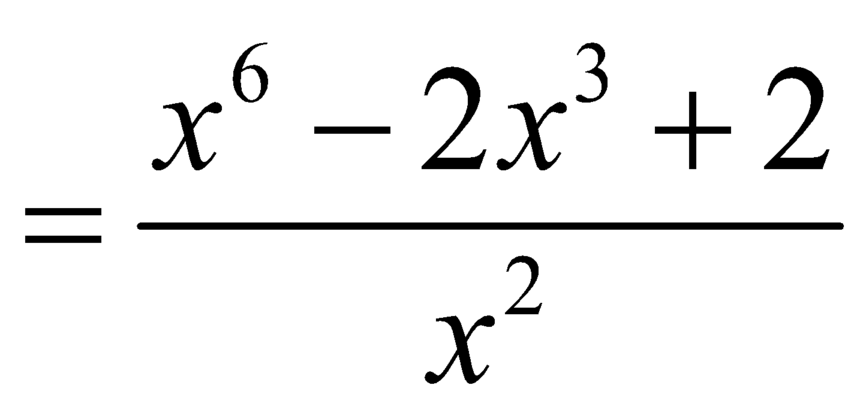
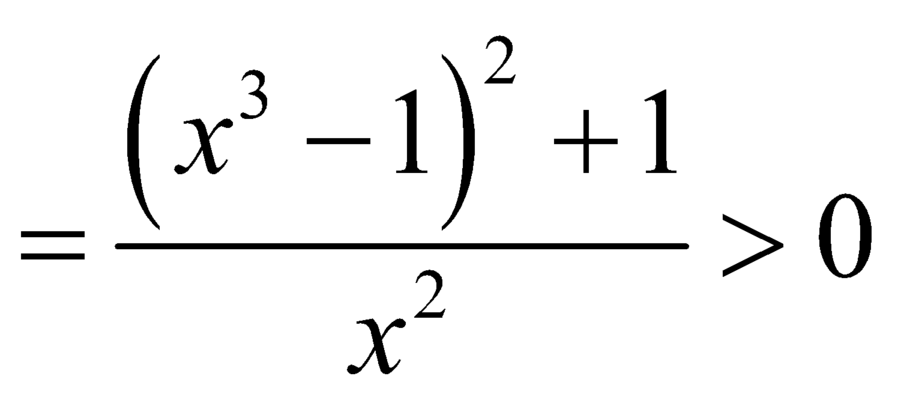đồng biến trên 
.
có nhiều nhất 
nghiệm trên khoảng 
.
Mặt khác ta có:
, 
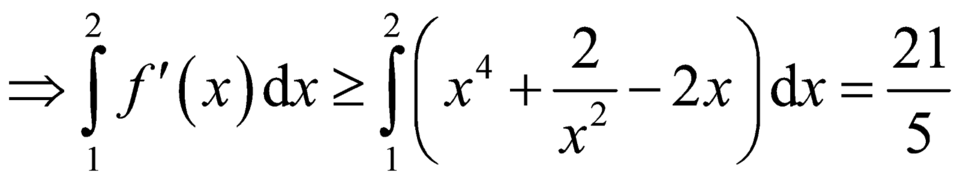
khoảng (1;2)
.
Kết hợp giả thiết ta có 
liên tục trên 
và 
.
Từ (1) và (2) suy ra phương trình f(x) = 0 có đúng 1 nghiệm trên khoảng (1;2)
CM
16 tháng 11 2019
Đáp án D
Ta có Đáp án D
Ta có y’ = –f’(1 – x) + 2018 = –[1–(1–x)][(1–x)+2]g(1–x) – 2018 + 2018
= –x(3–x)g(1–x)
Suy ra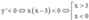 
(vì g(1–x) < 0,
∀
x
∈
R
)
Vậy hàm số đã cho nghịch biến trên khoảng 3 ; + ∞
AH
Akai Haruma
Giáo viên
15 tháng 4 2021
Lời giải:
Từ $f(1+3x)=2x-f(1-2x)$ thay $x=0$ suy ra $f(1)=1$
$f(1+3x)=2x-f(1-2x)$
$\Rightarrow f'(1+3x)=(2x)'-f'(1-2x)$
$\Leftrightarrow 3f'(1+3x)=2+2f'(1-2x)$. Thay $x=0$ suy ra $f'(1)=2$
PTTT của $f(x)$ tại điểm $x=1$ là:
$y=f'(1)(x-1)+f(1)=2(x-1)+1=2x-1$
\(f^2\left(1+2x\right)=x-f^3\left(1-2x\right)\)
Thay \(x=0\) vào ta được:
\(f^2\left(1\right)=-f^3\left(1\right)\Leftrightarrow f^2\left(1\right)\left[1+f\left(1\right)\right]=0\Rightarrow\left[{}\begin{matrix}f\left(1\right)=0\\f\left(1\right)=-1\end{matrix}\right.\)
Đạo hàm 2 vế:
\(\Rightarrow4f\left(1+2x\right).f'\left(1+2x\right)=1+6f^2\left(1-2x\right).f'\left(1-2x\right)\)
Thay \(x=0\) vào ta được:
\(4f\left(1\right).f'\left(1\right)=1+6f^2\left(1\right).f'\left(1\right)\)
- Nếu \(f\left(1\right)=0\Rightarrow0=1\) (loại)
- Nếu \(f\left(1\right)=-1\Rightarrow-4f'\left(1\right)=1+6f'\left(1\right)\Rightarrow f'\left(1\right)=-\frac{1}{10}\)