khoảng cách giữa 2 đường thẳng 3x - 4y - 18 = 0 đến đường thẳng 3x - 4y + 1 = 0 là bao nhiêu?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
19 tháng 12 2019
Ta có d 2 : 3 x − 2 y + 1 = 0 ⇔ 6 x − 4 y + 2 = 0
Ta có điểm A(-1; 1) thuộc đường thẳng d2,.
Vì hai đường thẳng d1 và d2 song song với nhau nên ta có:
d ( d 1 ; d 2 ) = d ( A ; d 1 ) = 6. ( − 1 ) − 4. ( − 1 ) + 5 6 2 + ( − 4 ) 2 = 3 52
ĐÁP ÁN D
PT
1
CM
8 tháng 12 2018
Áp dụng công thức tính khoảng cách từ 1 điểm đến 1 đường thẳng ta có:
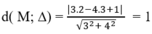
Chọn A.
PT
1
CM
17 tháng 10 2017
+ Giả sử M( x 0 ; y 0 ) ∈ C suy ra y 0 = 2 x 0 + 3 x 0 + 1
+Ta có
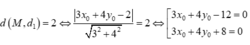
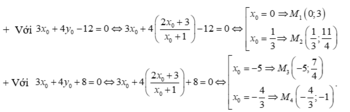
Ta tìm được 4 điểm M suy ra có 4 tiếp tuyến.
Chọn C.
CM
18 tháng 11 2018
- Giả sử 
- Ta có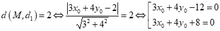 
- Với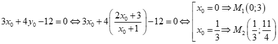 
- Với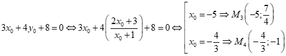 
Suy ra có 4 tiếp tuyến.
Chọn C.
CM
2 tháng 12 2018
ĐÁP ÁN C
d ( A ; Δ ) = a . x 0 + b y 0 + c a 2 + b 2 = 3.7 − 4.4 + 8 3 2 + ( − 4 ) 2 = 13 5
QT
1
HQ
Hà Quang Minh
Giáo viên
27 tháng 9 2023
Ta có vectơ pháp tuyến của hai đường thẳng là \(\overrightarrow {{n_1}} = \left( {3;4} \right),\overrightarrow {{n_2}} = \left( {6;8} \right)\) suy ra hai đường thẳng này song song, nên khoảng cách giữa chúng là khoảng cách từ một điểm bất kì từ đường thẳng này tới đường thẳng kia
Chọn điểm \(A\left( {0;\frac{5}{2}} \right) \in \Delta \), suy ra \(d\left( {\Delta ,\Delta '} \right) = d\left( {A,\Delta '} \right) = \frac{{\left| {6.0 + 8.\frac{5}{2} - 1} \right|}}{{\sqrt {{6^2} + {8^2}} }} = \frac{{19}}{{10}}\)
Vậy khoảng cách giữa hai đường thẳng \(\Delta :3x + 4y - 10 = 0\) và \(\Delta ':6x + 8y - 1 = 0\) là \(\frac{{19}}{{10}}\)
CM
23 tháng 6 2017
Lấy điểm O(0;0) nằm trên đường thẳng (b). Khi đó ta có:
Chọn B
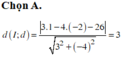
Gọi d là \(3x-4y-18=0\) và d' là \(3x-4y+1=0\)
Chọn \(A\left(6;0\right)\) là điểm thuộc d
\(\Rightarrow d\left(d;d'\right)=d\left(A;d'\right)=\frac{\left|3.6-4.0+1\right|}{\sqrt{3^2+\left(-4\right)^2}}=\frac{19}{5}\)
điển A(6,0) ở đâu ra vậy, hay là mk tự cho