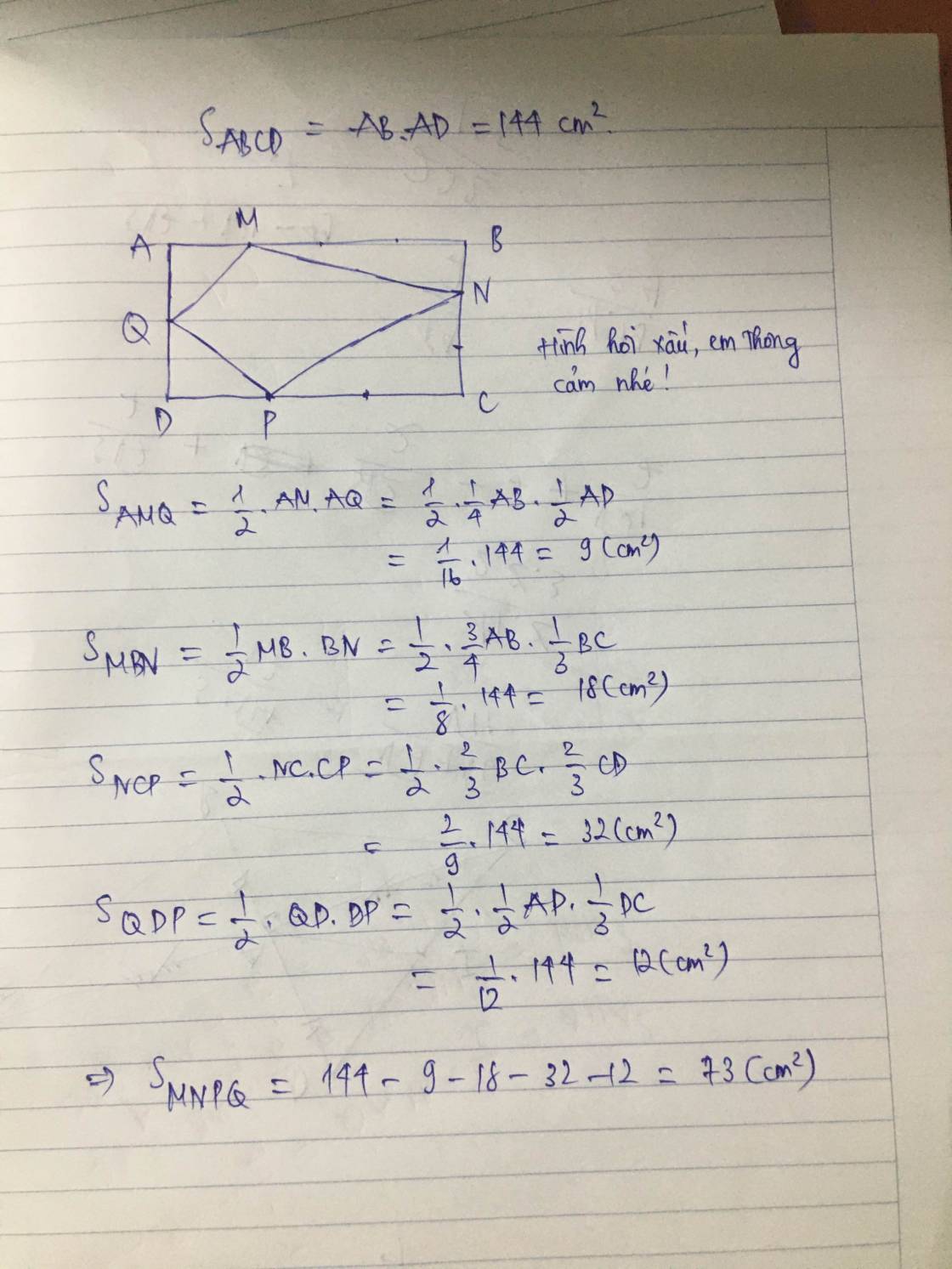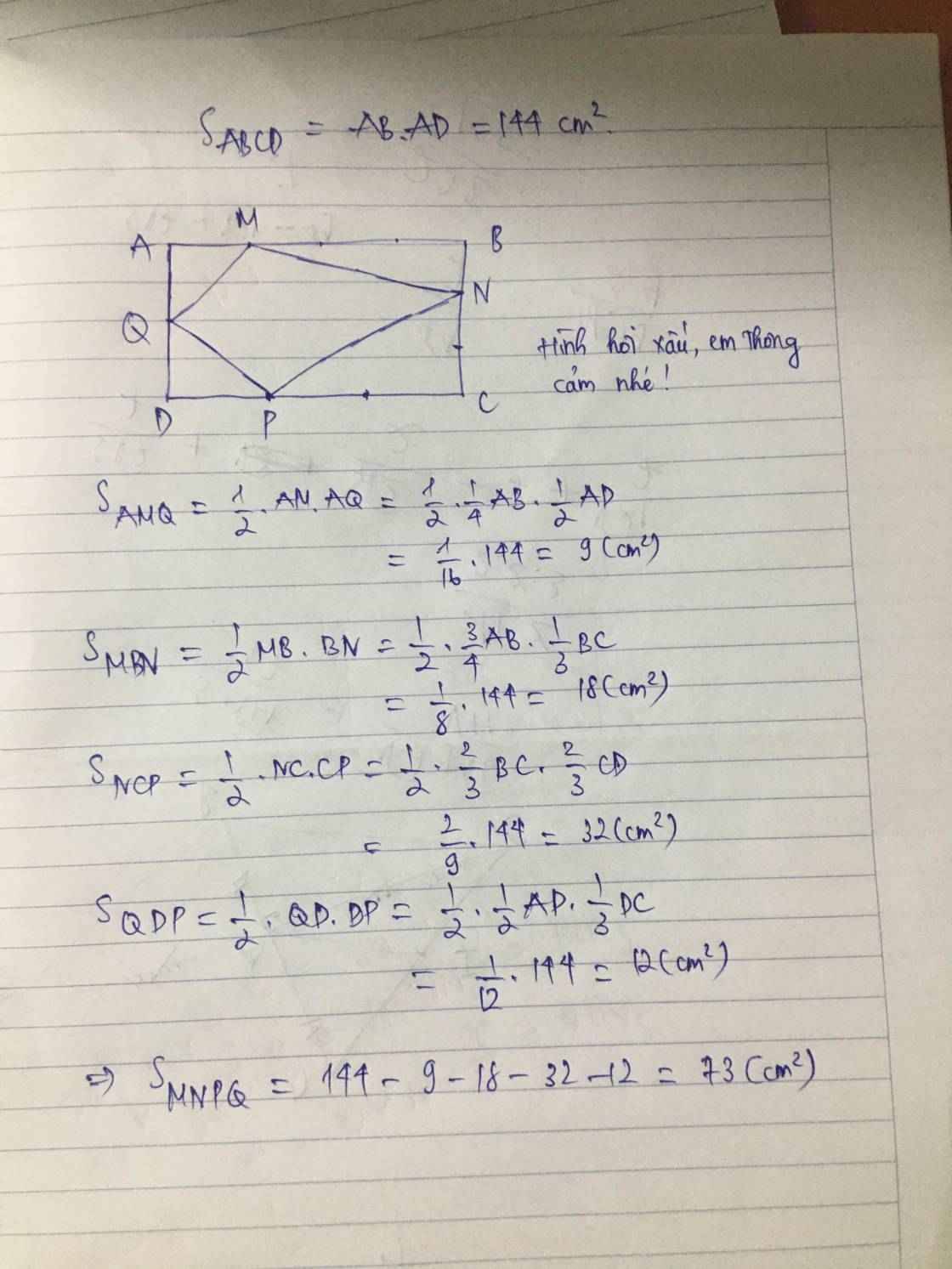Cho hình thang ABCD , trên AD lấy AM = DQ = 1/2 MQ . Trên BC lấy BN = PC=1/2 NP . Cho SMNPQ = 200 cm2 . Tính SABCD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
22 tháng 6 2023
SAMQ = \(\dfrac{1}{3}\)SABQ (vì hai tam giác có chung chiều cao hạ từ đỉnh Q xuống đáy AB và AM = \(\dfrac{1}{3}\)ABQ)
AQ = DA - QD = DA - \(\dfrac{1}{3}\)DA = \(\dfrac{2}{3}\)DA
SABQ = \(\dfrac{2}{3}\)SABD (vì hai tam giác có chung chiều cao hạ từ đỉnh B xuống đáy AD và QA = \(\dfrac{2}{3}\)DA)
SABD = \(\dfrac{1}{2}\) SABCD (vì ABCD là hình chữ nhật)
SAMQ = \(\dfrac{1}{3}\)\(\times\)\(\dfrac{2}{3}\)\(\times\)\(\dfrac{1}{2}\) \(\times\) SABCD = 162 \(\times\) \(\dfrac{1}{9}\) = 18 (cm2)
SBMN = \(\dfrac{2}{3}\)SBCM (vì hai tam giác có chung chiều cao hạ từ đỉnh M xuống đáy BC và BN = \(\dfrac{2}{3}\)BC)
BM = AB - AM = AB - \(\dfrac{1}{3}\)AB = \(\dfrac{2}{3}\)AB
SBCM = \(\dfrac{2}{3}\)SABC ( vì hai tam giác có chung chiều cao hạ từ đỉnh C xuống đáy AB và BM = \(\dfrac{2}{3}\)AB)
SABC = \(\dfrac{1}{2}\)SABCD ( vì ABCD là hình chữ nhật)
SBMN = \(\dfrac{2}{3}\times\dfrac{2}{3}\) \(\times\) \(\dfrac{1}{2}\)SABCD = 162 \(\times\) \(\dfrac{2}{9}\) = 36 (cm2)
CN = BC - BN = BC - \(\dfrac{2}{3}\)BC = \(\dfrac{1}{3}\)BC
SPCN = \(\dfrac{1}{3}\)SBPC( vì hai tam giác có cùng chiều cao hạ từ đỉnh P xuống đáy BC và CN = \(\dfrac{1}{3}\)BC
SPBC = \(\dfrac{2}{3}\)SBCD (vì hai tam giác có cùng chiều cao hạ từ đỉnh B xuống đáy CD và CP = \(\dfrac{2}{3}\)CD)
SBCD = \(\dfrac{1}{2}\)SABCD ( vì ABCD là hình chữ nhật)
SPCN = \(\dfrac{1}{3}\times\dfrac{2}{3}\times\dfrac{1}{2}\)SABCD = 162\(\times\)\(\dfrac{1}{9}\) = 18(cm2)
DP = DC - CP = DC - \(\dfrac{2}{3}\)DC = \(\dfrac{1}{3}\)DC
SDPQ = \(\dfrac{1}{3}\)SDCQ (vì hai tam giác có chung chiều cao hạ từ đỉnh Q xuống đáy DC và DP = \(\dfrac{1}{3}\)DC)
SDCQ = \(\dfrac{1}{3}\)SACD (vì hai tam giác có chung chiều cao hạ từ đỉnh C xuống đáy AD và DQ = \(\dfrac{1}{3}\)AD)
SADC = \(\dfrac{1}{2}\)SABCD ( vì ABCD là hình chữ nhật)
SDPQ = \(\dfrac{1}{3}\times\dfrac{1}{3}\times\dfrac{1}{2}\)SABCD = 162 \(\times\) \(\dfrac{1}{18}\) = 9 (cm2)
SMNPQ = SABCD - (SDPQ + SPCN + SBMN + SAQM)
SMNPQ = 162 - (9 + 18 + 36 + 18) = 81 (cm2)
Đáp số : 81 cm2
23 tháng 6 2023
Số viên bi Bình có là:
\(viên bi)
Tổng số viên bi của Bình và An là:
(viên bi)
Trung bình cộng số viên bi của 3 bạn là:
(viên bi)
Số viên bi của Thịnh là:
(viên bi)
Đáp số: ...
26 tháng 6 2023
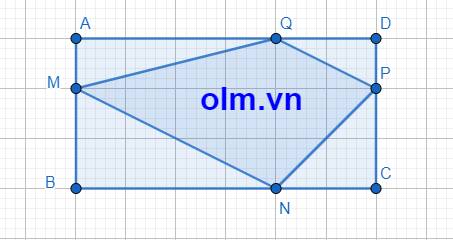
Ta thấy rằng \(\dfrac{BN}{BC}=\dfrac{AQ}{AD}\), mà \(BC=AD\) nên \(BN=AQ\), cũng có nghĩa ABNQ và CDQN là các hình chữ nhật. Ta kẻ MH và PK vuông góc với QN. Khi đó \(S_{MNPQ}=S_{MNQ}+S_{PNQ}\)
\(=\dfrac{1}{2}\times PQ\times MH+\dfrac{1}{2}\times PQ\times PK\)
\(=\dfrac{1}{2}\times PQ\times\left(MH+PK\right)\)
\(=\dfrac{1}{2}\times AB\times BC\) (do \(PQ=AB\) và \(MH+PK=BC\))
\(=\dfrac{1}{2}\times S_{ABCD}\)
\(=\dfrac{1}{2}\times324=162\left(cm^2\right)\)
24 tháng 6 2023
- Diện tích tam giác ABM là 1/2 * AB * AM = 1/2 * AB * 1/3 AB = 1/6 * AB^2
- Diện tích tam giác BCN là 1/2 * BC * BN = 1/2 * BC * 2/3 BC = 1/3 * BC^2
- Diện tích tam giác CDP là 1/2 * CD * CP = 1/2 * CD * PD = 1/6 * CD^2
- Diện tích tam giác DAQ là 1/2 * DA * DQ = 1/2 * DA * 1/3 DA = 1/6 * DA^2
Vậy tổng diện tích của 4 tam giác trên là:
1/6 * AB^2 + 1/3 * BC^2 + 1/6 * CD^2 + 1/6 * DA^2
- Đường chéo AC chia hình chữ nhật ABCD thành hai tam giác có diện tích lần lượt là 1/2 * AC * AB/2 = 1/4 * AC * AB và 1/2 * AC * CD/2 = 1/4 * AC * CD
- Đường chéo BD cũng chia hình chữ nhật ABCD thành hai tam giác có diện tích lần lượt là 1/2 * BD * BC/2 = 1/4 * BD * BC và 1/2 * BD * DA/2 = 1/4 * BD * DA
Do đó, ta có:
- Diện tích tam giác EFG là 1/2 * EF * EG = 1/2 * (AC/2) * (BD/2) = 1/8 * AC * BD
Vậy diện tích hình MNPQ bằng:
2 * diện tích tam giác EFG = 2 * 1/8 * AC * BD = 1/4 * AB * CD
Từ đó, ta suy ra diện tích hình MNPQ là 1/4 diện tích hình chữ nhật ABCD:
Diện tích hình MNPQ = 1/4 * 324 cm^2 = 81 cm^2
8 tháng 7 2023
` @ L I N H `
- Diện tích tam giác ABM là 1/2 * AB * AM = 1/2 * AB * 1/3 AB = 1/6 * AB^2
- Diện tích tam giác BCN là 1/2 * BC * BN = 1/2 * BC * 2/3 BC = 1/3 * BC^2
- Diện tích tam giác CDP là 1/2 * CD * CP = 1/2 * CD * PD = 1/6 * CD^2
- Diện tích tam giác DAQ là 1/2 * DA * DQ = 1/2 * DA * 1/3 DA = 1/6 * DA^2
Vậy tổng diện tích của 4 tam giác trên là:
1/6 * AB^2 + 1/3 * BC^2 + 1/6 * CD^2 + 1/6 * DA^2
- Đường chéo AC chia hình chữ nhật ABCD thành hai tam giác có diện tích lần lượt là 1/2 * AC * AB/2 = 1/4 * AC * AB và 1/2 * AC * CD/2 = 1/4 * AC * CD
- Đường chéo BD cũng chia hình chữ nhật ABCD thành hai tam giác có diện tích lần lượt là 1/2 * BD * BC/2 = 1/4 * BD * BC và 1/2 * BD * DA/2 = 1/4 * BD * DA
Do đó, ta có:
- Diện tích tam giác EFG là 1/2 * EF * EG = 1/2 * (AC/2) * (BD/2) = 1/8 * AC * BD
Vậy diện tích hình MNPQ bằng:
2 * diện tích tam giác EFG = 2 * 1/8 * AC * BD = 1/4 * AB * CD
Từ đó, ta suy ra diện tích hình MNPQ là 1/4 diện tích hình chữ nhật ABCD:
Diện tích hình MNPQ = 1/4 * 324 cm^2 = 81 cm^2
