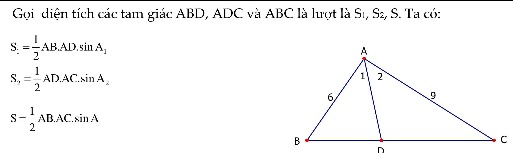
Tam giác ABC có AB=2, AC=3. AD là đường phân giác của góc BAC, AD=1,2. Tính góc BAC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Qua B kẻ đường thằng song song AD cắt CA tại E
Có \(\widehat{BAD}=\widehat{EBA}\left(slt\right);\widehat{DAC}=\widehat{E}\)(đồng vị)
Mà \(\widehat{BAD}=\widehat{DAC}\Rightarrow\widehat{EBA}=\widehat{E}\)
\(\Rightarrow\Delta BAE\)cân tại A \(\Rightarrow AB=AE=2\)
Sử dụng định lý Talet
\(\frac{AD}{EB}=\frac{AC}{EC}\Rightarrow\frac{1,2}{EB}=\frac{3}{AC+AE}\Rightarrow\frac{1,2}{EB}=\frac{3}{3+2}\Rightarrow\frac{1,2}{EB}=\frac{3}{5}\)
\(\Rightarrow EB=1,2:\frac{3}{5}=\frac{1,2\cdot5}{3}=\frac{6}{3}=2\)
\(\Rightarrow\Delta BAE\)đều => \(\widehat{BAE}=60^o\)
Mà \(\widehat{BAE}\)kề bù \(\widehat{BAC}\)\(\Rightarrow\widehat{BAC}=120^o\)


11:
\(AD=\dfrac{2\cdot AB\cdot AC}{AB+AC}\cdot cos60=\dfrac{2\cdot6\cdot12}{6+12}\cdot\dfrac{1}{2}=4\left(cm\right)\)
12:
\(AD=\dfrac{2\cdot AB\cdot AC}{AB+AC}\cdot cos60=\dfrac{2\cdot3\cdot6}{3+6}\cdot\dfrac{1}{2}=\dfrac{3\cdot6}{3+6}=\dfrac{18}{9}=2\left(cm\right)\)

a: AB<AC
=>góc B>góc C
góc ADB=góc DAC+góc ACD
góc ADC=góc BAD+góc ABD
mà góc ACD<góc ABD; góc BAD=góc CAD
nên góc ADB<góc ADC
b: Xét ΔABE có
AD vừa là đường cao, vừa là phân giác
=>ΔABE cân tại A
c: AD là phân giác
=>BD/AB=CD/AC
mà AB<AC
nên BD<CD

Theo tính chất tia phân giác của góc ta có:
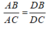
Suy ra:

Chọn đáp án D