Đề là chứng minh M N và P thẳng hàng nha cái chỗ khó nhìn là thoả mãn
Giúp mik với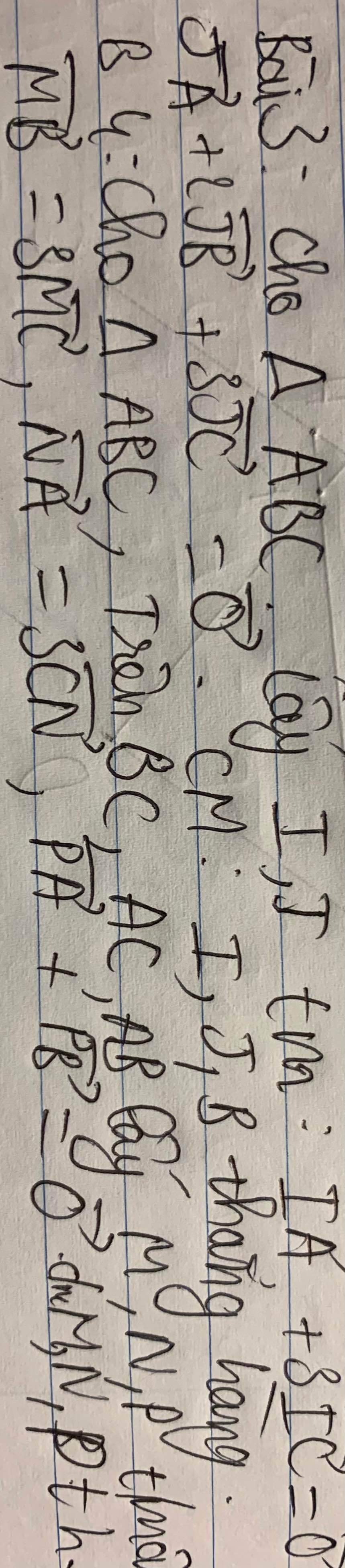
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1. chứng minh góc ABC là góc bẹt
2. chứng minh đoạn AB hoặc AC cùng song song vs 1 đoạn thẳng

Xét ΔBAD có BM là đường trung tuyến
nên \(\overrightarrow{BM}=\dfrac{1}{2}\left(\overrightarrow{BA}+\overrightarrow{BD}\right)\)
\(=\dfrac{1}{2}\left(\overrightarrow{BA}+\dfrac{2}{3}\overrightarrow{BC}\right)\)
\(=\dfrac{1}{2}\left(\overrightarrow{BA}+\dfrac{2}{3}\overrightarrow{BA}+\dfrac{2}{3}\overrightarrow{AC}\right)\)
\(=\dfrac{1}{2}\left(\dfrac{5}{3}\overrightarrow{BA}+\dfrac{2}{3}\overrightarrow{AC}\right)\)
\(=\dfrac{1}{6}\left(5\overrightarrow{BA}+2\overrightarrow{AC}\right)\)
\(=\dfrac{5}{6}\left(\overrightarrow{BA}+\dfrac{2}{5}\overrightarrow{AC}\right)\)
\(\overrightarrow{BN}=\overrightarrow{BA}+\overrightarrow{AN}\)
\(=\overrightarrow{BA}+\dfrac{2}{5}\overrightarrow{BC}\)
=>\(\overrightarrow{BM}=\dfrac{5}{6}\cdot\overrightarrow{BN}\)
=>B,M,N thẳng hàng

-Ta có:AC song song với BD
=>CAB = ABD(2 góc so le trong)
-Xét tam giác AMI và BMI,ta có:AM=BN(gt), CAB=ABD(gt), AI=IB(gt)
=>Hai tam giác AMI và BMI bằng nhau
=>MIA = NIB(2 góc tương ứng)
-Ta có:NIA + NIB =180 độ(2 góc kề bù)
-Mà MIA = NIB(cmt)
=>NIA + MIA =180 độ
=>MIN = 180 độ
=>M, I, N thẳng hàng
3.
\(\overrightarrow{IA}+3\overrightarrow{IC}=\overrightarrow{0}\Rightarrow\overrightarrow{IB}+\overrightarrow{BA}+3\overrightarrow{IB}+3\overrightarrow{BC}=\overrightarrow{0}\)
\(\Rightarrow4\overrightarrow{IB}+\overrightarrow{BA}+3\overrightarrow{BC}=\overrightarrow{0}\Rightarrow4\overrightarrow{IB}=\overrightarrow{AB}+3\overrightarrow{CB}\) (1)
\(\overrightarrow{JA}+2\overrightarrow{JB}+3\overrightarrow{JC}=\overrightarrow{0}\Rightarrow\overrightarrow{JB}+\overrightarrow{BA}+2\overrightarrow{JB}+3\overrightarrow{JB}+3\overrightarrow{BC}=\overrightarrow{0}\)
\(\Rightarrow6\overrightarrow{JB}+\overrightarrow{BA}+3\overrightarrow{BC}=0\Rightarrow6\overrightarrow{JB}=\overrightarrow{AB}+3\overrightarrow{CB}\) (2)
(1);(2) \(\Rightarrow4\overrightarrow{IB}=6\overrightarrow{JB}\Rightarrow\overrightarrow{IB}\) và \(\overrightarrow{JB}\) cùng phương
Hay I; J; B thẳng hàng
4.
\(\overrightarrow{PA}+\overrightarrow{PB}=\overrightarrow{0}\Rightarrow\overrightarrow{PA}+\overrightarrow{PA}+\overrightarrow{AB}=0\Rightarrow\overrightarrow{PA}=-\dfrac{1}{2}\overrightarrow{AB}\)
\(\overrightarrow{NA}=3\overrightarrow{CN}\Rightarrow\overrightarrow{NA}=3\overrightarrow{CA}+3\overrightarrow{AN}\Rightarrow4\overrightarrow{AN}=3\overrightarrow{AC}\)
\(\Rightarrow\overrightarrow{AN}=\dfrac{3}{4}\overrightarrow{AC}\)
\(\overrightarrow{MB}=3\overrightarrow{MC}\Rightarrow\overrightarrow{MB}=3\overrightarrow{MB}+3\overrightarrow{BC}\)
\(\Rightarrow2\overrightarrow{BM}=3\overrightarrow{BC}\Rightarrow\overrightarrow{BM}=\dfrac{3}{2}\overrightarrow{BC}=\dfrac{3}{2}\left(\overrightarrow{BA}+\overrightarrow{AC}\right)=-\dfrac{3}{2}\overrightarrow{AB}+\dfrac{3}{2}\overrightarrow{AC}\)
\(\Rightarrow\overrightarrow{PN}=\overrightarrow{PA}+\overrightarrow{AN}=-\dfrac{1}{2}\overrightarrow{AB}+\dfrac{3}{4}\overrightarrow{AC}\) (1)
\(\overrightarrow{PM}=\overrightarrow{PB}+\overrightarrow{BM}=\dfrac{1}{2}\overrightarrow{AB}-\dfrac{3}{2}\overrightarrow{AB}+\dfrac{3}{2}\overrightarrow{AC}=-\overrightarrow{AB}+\dfrac{3}{2}\overrightarrow{AC}=2\left(-\dfrac{1}{2}\overrightarrow{AB}+\dfrac{3}{4}\overrightarrow{AC}\right)\) (2)
(1);(2) \(\Rightarrow\overrightarrow{PM}=2\overrightarrow{PN}\Rightarrow\) P, M, N thẳng hàng