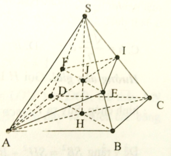
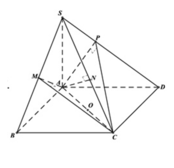
cho hình chóp đều S.ABCD. Mặt phẳng (P) qua A vuông góc với SC cắt AB, SC, SD lần lượt tại B', C', D'. Biết rằng \(AB=a,\frac{SB'}{SB}=\frac{2}{3}\) và C' nằm trên cạnh SC.
a, Tính diện tích AB'C'D'
b, Tính khoảng cách giữa hai đường thẳng AD và B'C'





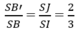
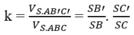




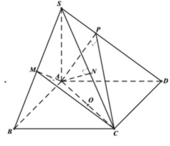


(P) cắt SB, SC, SD mới đúng, (P) đã cắt AB tại A rồi cơ mà
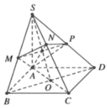
Từ A kẻ \(AC'\perp SC\), trong các mặt pẳng (SCD) và (SBC) từ C' lần lượt kẻ các đường thẳng vuông góc SC cắt SD và SB tại D' và B'
Gọi cạnh bên của hình chóp là \(SA=SB=SC=SD=x\Rightarrow SB'=\frac{2x}{3}\)
Áp dụng định lý hàm cos: \(cos\widehat{ASC}=\frac{2x^2-2a^2}{2x^2}\); \(cos\widehat{BSC}=\frac{2x^2-a^2}{2x^2}\)
Trong tam giác vuông SAC':\(SC'=SA.cos\widehat{ASC}=\frac{2x^2-2a^2}{2x}\)
Trong tam giác vuông SB'C': \(SC'=SB'.cos\widehat{BSC}=\frac{2x^2-a^2}{3x}\)
\(\Rightarrow\frac{2x^2-2a^2}{2x}=\frac{2x^2-a^2}{3x}\Rightarrow x=a\sqrt{2}\)
\(\Rightarrow SC'=\frac{a\sqrt{2}}{2}\Rightarrow\frac{SC'}{SC}=\frac{1}{2}\)
Do tính đối xứng của hình chóp đều \(\Rightarrow\frac{SD'}{SD}=\frac{SB'}{SB}=\frac{2}{3}\)
Áp dụng công thức Simsons ta có:
\(V_{S.AB'C'D'}=\frac{1}{4}.\frac{2}{3}.\frac{2}{3}.\frac{1}{2}\left(1+\frac{3}{2}+\frac{3}{2}+2\right)V_{S.ABCD}=\frac{1}{3}V_{SABCD}=\frac{a^3\sqrt{6}}{18}\)
\(\Rightarrow S_{AB'C'D'}=\frac{3V_{S.AB'C'D'}}{SC'}=\frac{a^2\sqrt{3}}{3}\)
b/Gọi O là tâm đáy, M là trung điểm BC \(\Rightarrow OM\perp BC\Rightarrow BC\perp\left(SOM\right)\)
\(AD//\left(SBC\right)\Rightarrow d\left(AD;B'C'\right)=d\left(AD;\left(SBC\right)\right)=2.d\left(O;\left(SBC\right)\right)\)
Từ O kẻ \(OH\perp SM\Rightarrow OH\perp\left(SBC\right)\Rightarrow OH=d\left(O;\left(SBC\right)\right)\)
\(SO=\frac{SC.\sqrt{3}}{2}=\frac{a\sqrt{6}}{2}\)
\(\frac{1}{OH^2}=\frac{1}{SO^2}+\frac{1}{OM^2}\Rightarrow OH=\frac{SO.OM}{\sqrt{SO^2+OM^2}}=\frac{a\sqrt{42}}{14}\)
\(\Rightarrow d\left(AD;B'C'\right)=\frac{a\sqrt{42}}{7}\)