Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/ Gọi M là trung điểm BC, nối SM cắt B'C' tại M'
Trong mặt phẳng (SAM), nối SG cắt A'M' tại Q
Q là giao điểm SG và (P)
b/ Ủa sao điểm D chẳng liên quan gì vậy ta, 2 câu rồi em nó vẫn bị ngó lơ.
Trong mặt phẳng (SCD), qua B và C lần lượt kẻ các đường thẳng song song SM, cắt B'C' kéo dài tại \(B_1\) và \(C_1\)
Áp dụng talet: \(\frac{BB_1}{SM'}=\frac{BB'}{SB'}\Rightarrow1+\frac{BB_1}{SM'}=\frac{BB'}{SB'}+1=\frac{SB}{SB'}\)
Tương tự ta có: \(1+\frac{CC_1}{SM'}=\frac{SC}{SC'}\)
Cộng vế với vế: \(2+\frac{BB_1+CC_1}{SM'}=\frac{SB}{SB'}+\frac{SC}{SC'}\)
Mà \(BB_1+CC_1=2MM'\) (t/c đường trung bình hình thang)
\(\Rightarrow2+\frac{2MM'}{SM'}=\frac{SB}{SB'}+\frac{SC}{SC'}\Rightarrow\frac{SB}{SB'}+\frac{SC}{SC'}=\frac{2\left(SM'+MM'\right)}{SM'}=\frac{2SM}{SM'}\)
Gọi N là trung điểm AM, trong mp (SAM), SN cắt A'M' tại N'
Hoàn toàn tương tự, ta có: \(\frac{SA}{SA'}+\frac{SM}{SM'}=\frac{2SN}{SN'}\)
\(\Rightarrow\frac{2SA}{SA'}+\frac{SB}{SB'}+\frac{SC}{SC'}=\frac{2SA}{SA'}+\frac{2SM}{SM'}=\frac{4SN}{SN'}\)
\(\Rightarrow\frac{4SN}{SN'}=8\Rightarrow SN'=\frac{1}{2}SN\)
\(\Rightarrow N'\) là trung điểm SN
Mà A; M; S cố định \(\Rightarrow N'\) cố định
\(\Rightarrow\left(P\right)\) luôn đi qua điểm N' cố định

\(\frac{BB'}{SB}=\frac{CC'}{SC}=\frac{1}{3}\Rightarrow B'C'//BC\Rightarrow B'C'//\left(ABC\right)\)
\(\frac{AA'}{SA}=\frac{CC'}{SC}=\frac{1}{3}\Rightarrow A'C'//AC\Rightarrow A'C'//\left(ABC\right)\)

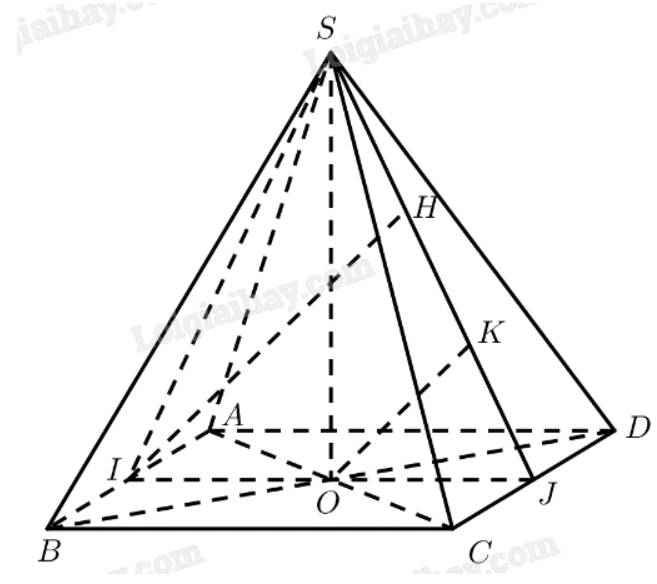
a) Gọi \(O\) là tâm của đáy
\( \Rightarrow SO \bot \left( {ABCD} \right) \Rightarrow SO \bot AB\)
\(I\) là trung điểm của \(AB\)
\(J\) là trung điểm của \(C{\rm{D}}\)
\( \Rightarrow IJ\) là đường trung bình của hình vuông \(ABCD\)
\(\left. \begin{array}{l} \Rightarrow IJ\parallel A{\rm{D}}\\AB \bot A{\rm{D}}\end{array} \right\} \Rightarrow IJ \bot AB\)
Ta có:
\(\left. \begin{array}{l}SO \bot AB\\IJ \bot AB\end{array} \right\} \Rightarrow AB \bot \left( {SIJ} \right)\)
b) Kẻ \(IH \bot SJ\left( {H \in SJ} \right),OK \bot SJ\left( {K \in SJ} \right) \Rightarrow IH\parallel OK\)
\(O\) là trung điểm của \(IJ \Rightarrow IH = 2{\rm{O}}K\)
Ta có:
\(\left. \begin{array}{l}AB\parallel C{\rm{D}}\\C{\rm{D}} \subset \left( {SC{\rm{D}}} \right)\end{array} \right\} \Rightarrow AB\parallel \left( {SC{\rm{D}}} \right) \Rightarrow d\left( {AB,SC} \right) = d\left( {AB,\left( {SC{\rm{D}}} \right)} \right)\)
\(\begin{array}{l}\left. \begin{array}{l}\left. \begin{array}{l}AB \bot \left( {SIJ} \right)\\C{\rm{D}}\parallel AB\end{array} \right\} \Rightarrow C{\rm{D}} \bot \left( {SIJ} \right) \Rightarrow C{\rm{D}} \bot IH\\ & IH \bot SJ\end{array} \right\} \Rightarrow IH \bot \left( {SC{\rm{D}}} \right)\\ \Rightarrow d\left( {AB,C{\rm{D}}} \right) = d\left( {AB,\left( {SC{\rm{D}}} \right)} \right) = IH\end{array}\)
\(O\) là trung điểm của \(IJ\), \(IH\parallel {\rm{O}}K\)\( \Rightarrow IH = 2{\rm{O}}K\)
\(O\) là trung điểm của \(B{\rm{D}}\)
\(J\) là trung điểm của \(C{\rm{D}}\)
\( \Rightarrow OJ\) là đường trung bình của \(\Delta BCD\)
\( \Rightarrow OJ = \frac{1}{2}BC = \frac{a}{2}\)
\(\Delta ABC\) vuông tại \(B\)\( \Rightarrow AC = \sqrt {A{B^2} + B{C^2}} = a\sqrt 2 \Rightarrow OA = \frac{1}{2}AC = \frac{{a\sqrt 2 }}{2}\)
\(\Delta SAO\) vuông tại \(O\)\( \Rightarrow SO = \sqrt {S{A^2} - O{A^2}} = \frac{{a\sqrt 6 }}{2}\)
\(\Delta SOJ\) vuông tại \(O\) có đường cao \(OK\)
\( \Rightarrow OK = \frac{{SO.OJ}}{{\sqrt {S{O^2} + O{J^2}} }} = \frac{{a\sqrt {42} }}{{14}}\)
\( \Rightarrow d\left( {AB,C{\rm{D}}} \right) = IH = 2OK = \frac{{a\sqrt {42} }}{7}\)
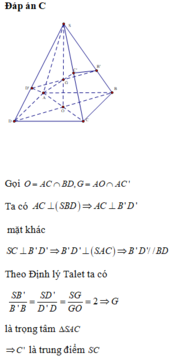
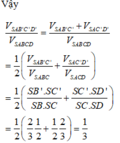
(P) cắt SB, SC, SD mới đúng, (P) đã cắt AB tại A rồi cơ mà
Từ A kẻ \(AC'\perp SC\), trong các mặt pẳng (SCD) và (SBC) từ C' lần lượt kẻ các đường thẳng vuông góc SC cắt SD và SB tại D' và B'
Gọi cạnh bên của hình chóp là \(SA=SB=SC=SD=x\Rightarrow SB'=\frac{2x}{3}\)
Áp dụng định lý hàm cos: \(cos\widehat{ASC}=\frac{2x^2-2a^2}{2x^2}\); \(cos\widehat{BSC}=\frac{2x^2-a^2}{2x^2}\)
Trong tam giác vuông SAC':\(SC'=SA.cos\widehat{ASC}=\frac{2x^2-2a^2}{2x}\)
Trong tam giác vuông SB'C': \(SC'=SB'.cos\widehat{BSC}=\frac{2x^2-a^2}{3x}\)
\(\Rightarrow\frac{2x^2-2a^2}{2x}=\frac{2x^2-a^2}{3x}\Rightarrow x=a\sqrt{2}\)
\(\Rightarrow SC'=\frac{a\sqrt{2}}{2}\Rightarrow\frac{SC'}{SC}=\frac{1}{2}\)
Do tính đối xứng của hình chóp đều \(\Rightarrow\frac{SD'}{SD}=\frac{SB'}{SB}=\frac{2}{3}\)
Áp dụng công thức Simsons ta có:
\(V_{S.AB'C'D'}=\frac{1}{4}.\frac{2}{3}.\frac{2}{3}.\frac{1}{2}\left(1+\frac{3}{2}+\frac{3}{2}+2\right)V_{S.ABCD}=\frac{1}{3}V_{SABCD}=\frac{a^3\sqrt{6}}{18}\)
\(\Rightarrow S_{AB'C'D'}=\frac{3V_{S.AB'C'D'}}{SC'}=\frac{a^2\sqrt{3}}{3}\)
b/Gọi O là tâm đáy, M là trung điểm BC \(\Rightarrow OM\perp BC\Rightarrow BC\perp\left(SOM\right)\)
\(AD//\left(SBC\right)\Rightarrow d\left(AD;B'C'\right)=d\left(AD;\left(SBC\right)\right)=2.d\left(O;\left(SBC\right)\right)\)
Từ O kẻ \(OH\perp SM\Rightarrow OH\perp\left(SBC\right)\Rightarrow OH=d\left(O;\left(SBC\right)\right)\)
\(SO=\frac{SC.\sqrt{3}}{2}=\frac{a\sqrt{6}}{2}\)
\(\frac{1}{OH^2}=\frac{1}{SO^2}+\frac{1}{OM^2}\Rightarrow OH=\frac{SO.OM}{\sqrt{SO^2+OM^2}}=\frac{a\sqrt{42}}{14}\)
\(\Rightarrow d\left(AD;B'C'\right)=\frac{a\sqrt{42}}{7}\)