Số điểm cực trị của hàm số y=x2016 *(x2+1)2017là
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
19 tháng 2 2017
Chọn đáp án B
Phương pháp
Số điểm cực trị của hàm số y=f(x) là số nghiệm bội lẻ của phương trình f’(x)=0.
Cách giải
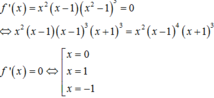
Tuy nhiên x=0 là nghiệm bội 2, x=1 là nghiệm bội 4 của phương trình f’(x)=0, do đó chúng không là cực trị của hàm số. Vậy hàm số có duy nhất 1 điểm cực trị x=-1.
Chú ý: HS nên phân tích đa thức f’(x) thành nhân tử triệt để trước khi xác định nghiệm, tránh sai lầm khi kết luận x=1 cũng là cực trị của hàm số.
PT
1
CM
20 tháng 12 2019
Đáp án C.
Cách 1: Tập xác định: D = ℝ
Ta có:
y = x 3 − x 2 − x + 1 = x 6 − x 2 − x 2 + 1
⇒ y ' = 6 x 5 2 x 6 − 2 x − 2 x 2 x 2 = 3 x 5 − 2 x x 6 − x . x 4 x 6
Ta thấy y' không xác định tại x=0.
- Nếu x > 0 : y ' = 3 x 2 − 2 x 4 − x 3 x 3 = 3 x 2 − 2 x − 1 ; y ' = 0 ⇒ x = 1 .
- Nếu x < 0 :
y ' = 3 x 5 + 2 x 4 − x 3 − x 3 = − 3 x 2 − 2 x + 1 y ' = 0 ⇒ x = − 1
Bảng biến thiên:
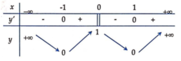
Hàm số đã cho có 3 điểm cực trị.
Cách 2: Đặt t = x , t ≥ 0 . Xét hàm số f t = t 3 − t 2 − t + 1, t ≥ 0 .
Ta có:
f ' t = 3 t 2 − 2 t − 1 ; f ' t = 0 ⇔ t = 0
Bảng biến thiên của hàm số f(t):
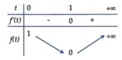
Ta có hàm số y = x 3 − x 2 − x + 1 là hàm số chẵn (đồ thị đối xứng qua trục Oy).
Suy ra bảng biến thiên của hàm số y = x 3 − x 2 − x + 1 :
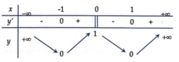
Do đó hàm số y = x 3 − x 2 − x + 1 có 3 điểm cực trị.
CM
30 tháng 10 2018
Đáp án A
Phương pháp giải:
Tìm tọa độ điểm cực trị của đồ thị hàm số trùng phương và tính diện tích tam giác
Lời giải: TXĐ : D = R
Ta có 
R
Phương trình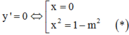 
Hàm số có 3 điểm cực trị ó (*) có 2 nghiệm phân biệt khác 
Khi đó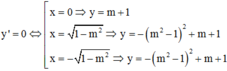 
Gọi 
; 
là ba điểm cực trị. Tam giác ABC cân tại A.
Trung điểm H của BC là 
Và 
Diện tích tam giác ABC là 
Mà 
R suy ra 
Vậy Smax = 1 Dấu bằng xảy ra khi và chỉ khi m = 0
CM
24 tháng 9 2019
Chọn C
[Phương pháp tự luận]
Hàm số có cực đại , cực tiểu khi và chỉ khi m < 1
Tọa độ điểm cực trị A ( 0 ; m + 1 )
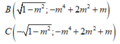
Phương trình đường thẳng BC: y + m 4 - 2 m 2 - m = 0
Vậy S đạt giá trị lớn nhất ⇔ m = 0
[Phương pháp trắc nghiệm]
Vậy S đạt giá trị lớn nhất ⇔ m = 0
CM
7 tháng 3 2019
Đáp án D
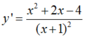
Gọi x1, x2 là hoành độ hai điểm cực trị.
Khi đó x1, x2 là hai nghiệm của phương trình y’ = 0
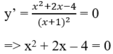
Theo định lý Vi-et, ta có x1.x2 = -4
CM
24 tháng 4 2018
Đáp án D.
Tập xác định D = R \ {2}
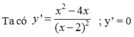
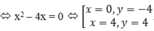
Bảng biến thiên
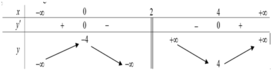
Dựa vào bảng biến thiên, số điểm cực trị của hàm số đã cho là 2
\(y'=2016x^{2015}.\left(x^2+1\right)^{2017}+2017\left(x^2+1\right)^{2016}.2x.x^{2016}\)
\(y'=x^{2015}\left(x^2+1\right)^{2016}\left(2016\left(x^2+1\right)+2017.2x^2\right)\)
\(y'=x^{2015}\left(x^2+1\right)^{2016}\left(2016x^2+2016+2017.2x^2\right)\)
\(y'=0\Rightarrow x=0\)
Hàm số có 1 cực trị duy nhất