Tam giác ABC có ∠B=450;∠C=1200 . Trên tia đối của tia CB lấy điểm D sao cho CD=2CB. Tính ∠ADB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
11 tháng 3 2019
Ta có: ∠A + ∠B + ∠C = 180 0
⇒ ∠A = 180 0 - ∠B - ∠C = 180 0 - 65 0 - 45 0 = 70 0
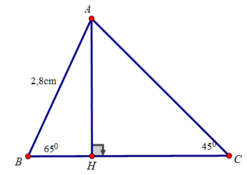
Kẻ đường cao AH
Xét tam giác ABH vuông tại H có:
AH = AB.sin B = 2,8.sin 65o ≈ 2,54 cm
BH = AB.cos 65o = 2,8.cos 65o ≈ 1,18 cm
Xét tam giác AHC vuông tại H có:
HC = AH.cotg C = 2,54.cotg 45 0 ≈ 2,54 cm
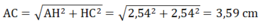
Ta có: BC = BH + HC = 1,18 + 2,54 = 3,72 cm
Vậy ∠A = 70 0 ; AC = 3,59 cm; BC= 3,72 cm
P
2
28 tháng 6 2021
\(\dfrac{a}{SinA}=\dfrac{b}{SinB}=\dfrac{c}{SinC}\)
\(\Rightarrow\dfrac{4}{Sin105}=\dfrac{AC}{Sin45}=\dfrac{AB}{Sin30}=4\sqrt{6}-4\sqrt{2}\)
\(\Rightarrow\left\{{}\begin{matrix}AB=2\sqrt{6}-2\sqrt{2}\\AC=-4+4\sqrt{3}\end{matrix}\right.\) ( cm )
Vậy ..
28 tháng 6 2021
Vẽ đường cao AH
Ta có: ΔAHB vuông tại H(gt)
mà \(\widehat{B}=45^0\)
nên ΔAHB vuông cân tại H
⇔\(BH=AH=HC\cdot\tan30^0\)
\(\Leftrightarrow BH-CH\cdot\tan30^0=\dfrac{CH}{\sqrt{3}}\)
\(\Leftrightarrow BH=\dfrac{4}{1+\sqrt{3}}\)
\(\Leftrightarrow AB=\dfrac{AH}{\sin45^0}\simeq2,06\left(cm\right)\)
\(\Leftrightarrow AC=2\cdot AH=2,92\left(cm\right)\)
CM
19 tháng 6 2018
Đáp án C
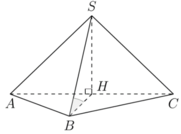
Gọi H là trung điểm AC. Ta có tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với (ABC)
suy ra S H ⊥ A B C
Ta có
S B , A B C = S B H ^ = 45 o ⇒ S H = B H = 1 2 A C = a 2 2 V S . A B C = 1 3 . a 2 2 . 1 2 a 2 = a 3 2 12
CT
1
YN
27 tháng 12 2021
Answer:
Ta xét tam giác ABC
AB = AC (gt)
=> Tam giác ABC cân tại A
\(\Rightarrow\widehat{ABC}=\widehat{ACB}\)
Ta có: \(\widehat{BAC}+\widehat{ABC}+\widehat{BCA}=180^o\)
Mà \(\widehat{ABC}=\widehat{ACB}\) (chứng minh trên)
\(\Rightarrow\widehat{BAC}+2\widehat{ABC}=180^o\)
\(\Rightarrow2\widehat{ABC}=180^o-\widehat{BAC}\)
\(\Rightarrow\widehat{ABC}=\widehat{ACB}=\frac{180^o-50^o}{2}=\frac{130^o}{2}=65^o\)
