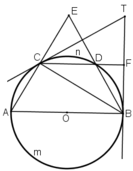
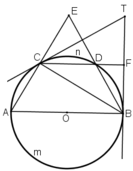
Trên một đường tròn lấy liên tiếp 3 cung AC,CD,DB sao cho sđ \(\stackrel\frown{AC}\)=sđ\(\stackrel\frown{CD}\)=sđ\(\stackrel\frown{DB}\)=60\(\)độ. Hai đường thẳng AC và BD cắt nhau ở E. Hai tiếp tuyến của đường tròn tại B và C cắt nhau. Chứng minh rằng:
a. \(\widehat{AEB}\) =\(\widehat{BTC}\).
b. Chứng minh CD là tia phân giác của góc BCI

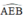 là góc có đỉnh ở ngoài đường tròn chắn hai cung
là góc có đỉnh ở ngoài đường tròn chắn hai cung 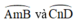
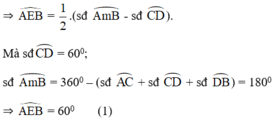
 là góc có đỉnh ở ngoài đường tròn chắn hai cung
là góc có đỉnh ở ngoài đường tròn chắn hai cung 

 là góc tạo bởi tiếp tuyến CT và dây CD
là góc tạo bởi tiếp tuyến CT và dây CD