Tính diện tích tứ giác ABCD theo AC,BD,biết AC(...chỗ này có cái dấu chữ T ngược..)BD tại H
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
19 tháng 12 2021
a: Xét ΔABD có
E là trung điểm của AB
H là trung điểm của AD
Do đó: EH là đường trung bình
=>EH//BD và EH=BD/2(1)
Xét ΔBCD có
F là tđiểm của BC
G là tđiểm của CD
Do đó: FG là đường trung bình
=>FG//BD và FG=BD/2(2)
Xét ΔADC có
H là tđiểm của AD
G là tđiểm của CD
Do đó: GH là đường trung bình
=>GH⊥EH(3)
Từ (1), (2) và (3) suy ra EFGH là hình chữ nhật
CM
30 tháng 5 2017
Phương pháp:
Sử dụng các công thức diện tích tam giác 
và công thức Cosin 
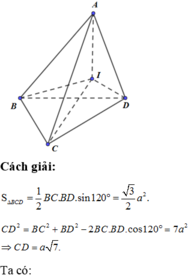
Cách giải:
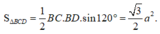
Ta có: 
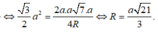
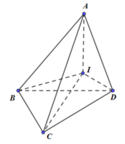
Gọi I là tâm đường tròn ngoại tiếp tam giác BCD.
Do AB = AC = AD 
Thể tích tứ diện ABCD là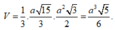 
Chọn D.
AH
Akai Haruma
Giáo viên
4 tháng 7 2021
Lời giải:
Vận dụng bổ đề $S_{ABC}=\frac{1}{2}.AB.AC\sin A$ ta có:
$S_{ABCD}=S_{OAB}+S_{OBC}+S_{ODC}+S_{AOD}$
$=\frac{1}{2}.OA.OB.\sin \widehat{AOB}+\frac{1}{2}.OB.OC.\sin \widehat{BOC}+\frac{1}{2}.OD.OC.\sin \widehat{DOC}+\frac{1}{2}.OA.OD.\sin \widehat{AOD}$
$=\frac{1}{2}.OA.OB\sin 60^0+\frac{1}{2}.OB.OC.\sin 120^0+\frac{1}{2}.OD.OC\sin 60^0+\frac{1}{2}.OA.OD.\sin 120^0$
$=\frac{\sqrt{3}}{4}(OA.OB+OB.OC+OC.OD+OD.OA)$
$=\frac{\sqrt{3}}{4}(AC.BD)=\frac{\sqrt{3}}{4}.4.5=5\sqrt{3}$ (cm vuông)
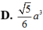
\(^SABC=\frac{1}{2}BH.AC\)
\(^SADC=\frac{1}{2}DH.AC\)
\(^SABCD=^SABC+^SADC=\frac{1}{2}BH.AC+\frac{1}{2}DH.AC\)
\(=\frac{1}{2}\left(BH+DH\right).AC=\frac{1}{2}BD.AC\)
Tôi chỉ biết vậy thôi chứ tôi mới lớp 6 ề!