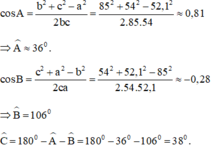Tính các góc của tam giác ABC . Biết rằng Â= 2B̂ = 3C
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Theo định lý tổng ba góc trong tam giác ABC, ta có:
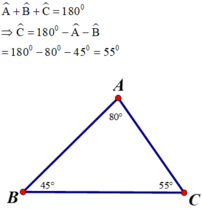
Cạnh đối diện góc B là AC
Cạnh đối diện góc C là AB
Cạnh đối diện góc A là BC
Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn.
Vì 450 < 550 < 800 hay B̂ < Ĉ < Â ⇒ AC < AB < BC.
Cho tam giác ABC có Â = 120o, cạnh b = 8cm và c = 5cm. Tính cạnh a, các góc B̂, Ĉ của tam giác đó.

+ a2 = b2 + c2 - 2.bc.cosA = 82 + 52 – 2.5.8.cos120º = 129
⇒ a = √129 cm
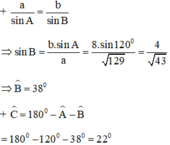

Bài 1:
a=2b=3c
=>a/6=b/3=c/2
Áp dụng tính chất của DTSBN, ta được:
\(\dfrac{a}{6}=\dfrac{b}{3}=\dfrac{c}{2}=\dfrac{a+b+c}{6+3+2}=\dfrac{180}{11}\)
=>a=1080/11; b=540/11; c=360/11

a:
Áp dụng tính chất của dãy tỉ số bằng nhau,ta được:
\(\dfrac{a}{\dfrac{1}{6}}=\dfrac{b}{\dfrac{1}{14}}=\dfrac{c}{\dfrac{1}{21}}=\dfrac{a+b+c}{\dfrac{1}{6}+\dfrac{1}{14}+\dfrac{1}{21}}=\dfrac{180}{\dfrac{2}{7}}=630\)
Do đó: a=105; b=45; c=30

\(a,\Delta ABC\) có \(\widehat{A}+\widehat{B}+\widehat{C}=180\) mà \(\widehat{A}=180-3\widehat{C}\)
\(\Rightarrow\widehat{B}+\widehat{C}=180-\widehat{A}=3C\\ \Rightarrow\widehat{B}=2\widehat{C}\)
Thay \(\widehat{B}=80\Rightarrow\widehat{C}=\dfrac{80}{2}=40\Rightarrow\widehat{A}=180-3\cdot40=60\)
\(b,\) Ta có \(DE//BC\)
\(\Rightarrow\widehat{EBC}=\widehat{DEB}\left(SLT\right)\)
Ta có \(\widehat{AEB}=\widehat{C}+\widehat{EBC}=\widehat{C}+\dfrac{1}{2}\widehat{B}=\widehat{C}+\dfrac{1}{2}\cdot2\widehat{C}=2\widehat{C}=\widehat{B}\)
(vì \(\widehat{AEB}\) là góc ngoài \(\Delta EBC\))
\(\Rightarrow\widehat{AED}+\widehat{DEB}=\widehat{ABE}+\widehat{EBC}\)
Mà \(\widehat{EBC}=\widehat{DEB}\left(cmt\right)\)
\(\Rightarrow\widehat{AED}=\widehat{ABE}\)
Mà \(\widehat{EBC}=\widehat{ABE}\left(GT\right)\)
\(\Rightarrow\widehat{DEB}=\widehat{AED}\)
Vậy \(ED\) là phân giác \(\widehat{AEB}\)

Áp dụng định lý côsin ta có:
BC2 = AB2 + AC2 – 2.AB.AC.cos A
= m2 + n2 – 2.m.n.cos120º
= m2 + n2 + mn.
⇒ BC = √( m2 + n2 + mn).