PT
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
CM
15 tháng 8 2018
Theo định lý tổng ba góc trong tam giác ABC, ta có:
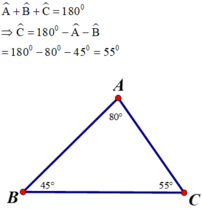
Cạnh đối diện góc B là AC
Cạnh đối diện góc C là AB
Cạnh đối diện góc A là BC
Trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn.
Vì 450 < 550 < 800 hay B̂ < Ĉ < Â ⇒ AC < AB < BC.
12 tháng 1 2023
Bài 1:
a=2b=3c
=>a/6=b/3=c/2
Áp dụng tính chất của DTSBN, ta được:
\(\dfrac{a}{6}=\dfrac{b}{3}=\dfrac{c}{2}=\dfrac{a+b+c}{6+3+2}=\dfrac{180}{11}\)
=>a=1080/11; b=540/11; c=360/11
5 tháng 11 2021
a:
Áp dụng tính chất của dãy tỉ số bằng nhau,ta được:
\(\dfrac{a}{\dfrac{1}{6}}=\dfrac{b}{\dfrac{1}{14}}=\dfrac{c}{\dfrac{1}{21}}=\dfrac{a+b+c}{\dfrac{1}{6}+\dfrac{1}{14}+\dfrac{1}{21}}=\dfrac{180}{\dfrac{2}{7}}=630\)
Do đó: a=105; b=45; c=30
NN
2
30 tháng 10 2016
cho tam giác ABC đường cao AH trên nửa mặt phẳg bò AC không chứa B.Vẽ tam giac ACD sao cho AD=BC
CM: AB song song CD
AH vuông góc AD
TA
5 tháng 7 2016
Vì AD là tia phân giác góc A => góc BAD = góc CAD ( gọi chung là A1 nhé )
Vì góc ADB = 80độ => góc ADC = 180độ ( 2 góc kề bù nhé )
Xét tam giác ABD có góc B = 100độ - A1
Xét tam giác ACD có góc C = 80độ -A1
MÀ 2B = 3C =>>>>> 200độ -2A1 = 240độ -3A1 => 3A1-2A1 = 240độ - 200độ =>A1=40độ hay : góc BAD = góc CAD = A1 = 40độ
Từ đó =>>>>>>>>>>>>>>>>>> góc A = 80độ ; góc B = 60độ ; góc C = 40độ (k cho mink nha )))))))))))THANKS NHÌU
8 tháng 8 2016
Tổng số đo các góc của hình tam giác luôn bằng 360 độ
Số đo của góc A là:360:(3+5+7)x3=72 độ
Số đo của góc B là:72:3x5=120 độ
Số đo của góc C là:360-120-72=168 độ
28 tháng 8 2021
\(a,\Delta ABC\) có \(\widehat{A}+\widehat{B}+\widehat{C}=180\) mà \(\widehat{A}=180-3\widehat{C}\)
\(\Rightarrow\widehat{B}+\widehat{C}=180-\widehat{A}=3C\\ \Rightarrow\widehat{B}=2\widehat{C}\)
Thay \(\widehat{B}=80\Rightarrow\widehat{C}=\dfrac{80}{2}=40\Rightarrow\widehat{A}=180-3\cdot40=60\)
\(b,\) Ta có \(DE//BC\)
\(\Rightarrow\widehat{EBC}=\widehat{DEB}\left(SLT\right)\)
Ta có \(\widehat{AEB}=\widehat{C}+\widehat{EBC}=\widehat{C}+\dfrac{1}{2}\widehat{B}=\widehat{C}+\dfrac{1}{2}\cdot2\widehat{C}=2\widehat{C}=\widehat{B}\)
(vì \(\widehat{AEB}\) là góc ngoài \(\Delta EBC\))
\(\Rightarrow\widehat{AED}+\widehat{DEB}=\widehat{ABE}+\widehat{EBC}\)
Mà \(\widehat{EBC}=\widehat{DEB}\left(cmt\right)\)
\(\Rightarrow\widehat{AED}=\widehat{ABE}\)
Mà \(\widehat{EBC}=\widehat{ABE}\left(GT\right)\)
\(\Rightarrow\widehat{DEB}=\widehat{AED}\)
Vậy \(ED\) là phân giác \(\widehat{AEB}\)