\(\frac{3^2}{8.11}\) +\(\frac{3^2}{11.14}\)+\(\frac{3^2}{14.17}\)+...+\(\frac{3^2}{197.200}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(B=\frac{9}{8\cdot11}+\frac{9}{11\cdot14}+...+\frac{9}{197\cdot200}\)
\(=3\left(\frac{3}{8\cdot11}+\frac{3}{11\cdot14}+...+\frac{3}{197\cdot200}\right)\)
\(=3\left(\frac{1}{8}-\frac{1}{11}+\frac{1}{11}-\frac{1}{14}+...+\frac{1}{197}-\frac{1}{200}\right)\)
\(=3\left(\frac{1}{8}-\frac{1}{200}\right)\)
\(=3\left(\frac{24}{200}-\frac{1}{200}\right)\)
\(=3\cdot\frac{23}{200}\)
đúng

\(\left[\frac{2000}{2000.2006}+\frac{2000}{2006.2012}+...+\frac{2000}{2492.2498}\right]\times\left[\frac{3^2}{8.11}+\frac{3^2}{11.14}+\frac{3^2}{14.17}+...+\frac{3^2}{197.200}\right]\)
\(=\left[\frac{2000}{6}\cdot\left(\frac{1}{2000}-\frac{1}{2006}+...+\frac{1}{2492}-\frac{1}{2498}\right)\right]\times\left[\frac{9}{8.11}+\frac{9}{11.14}+...+\frac{9}{197.200}\right]\)
\(=\left[\frac{2000}{6}\cdot\left(\frac{1}{2000}-\frac{1}{2498}\right)\right]\times\left[\frac{9}{3}\cdot\left(\frac{1}{8}-\frac{1}{11}+\frac{1}{11}-\frac{1}{14}+..+\frac{1}{197}-\frac{1}{200}\right)\right]\)
\(=\left[\frac{2000}{6}\cdot\frac{498}{4996000}\right]\times\left[\frac{9}{3}\cdot\left(\frac{1}{8}-\frac{1}{200}\right)\right]\)
\(=\frac{83}{2498}\times\left[\frac{9}{3}\cdot\frac{3}{25}\right]\)
\(=\frac{83}{2498}\times\frac{9}{25}=\frac{747}{62450}\)

lúc đầu ý bn là 5/1.3 đúng k, mk chỉnh lại như thế cho tiện nhé
a) \(\frac{5}{1\times3}+\frac{5}{3\times5}+\frac{5}{5\times7}+...+\frac{5}{99\times101}\)
\(=\frac{5}{2}\left(\frac{1}{1}-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+...+\frac{1}{99}-\frac{1}{101}\right)\)
\(=\frac{5}{2}\left(1-\frac{1}{101}\right)\)
\(=\frac{5}{2}\times\frac{100}{101}=\frac{250}{101}\)
b) \(\frac{3^2}{8\times11}+\frac{3^2}{11\times14}+\frac{3^2}{14\times17}+...+\frac{3^2}{197\times200}\)
\(=\frac{9}{8\times11}+\frac{9}{11\times14}+\frac{9}{14\times17}+...+\frac{9}{197\times200}\)
\(=3\left(\frac{1}{8}-\frac{1}{11}+\frac{1}{11}-\frac{1}{14}+\frac{1}{14}-\frac{1}{17}+...+\frac{1}{197}-\frac{1}{200}\right)\)
\(=3\left(\frac{1}{8}-\frac{1}{200}\right)\)
\(=3\times\frac{3}{25}=\frac{9}{25}\)
Ta có \(\frac{3^2}{8.11}+\frac{3^2}{11.14}+...+\frac{3^2}{197.200}\)
\(\Rightarrow3^2.\left(\frac{1}{8.11}+\frac{1}{11.14}+...+\frac{1}{197.200}\right)\)
\(\Rightarrow9.\frac{1}{3}.\left(\frac{1}{8}-\frac{1}{11}+\frac{1}{11}-\frac{1}{14}+...+\frac{1}{197}-\frac{1}{200}\right)\)
\(\Rightarrow3.\left(1-\frac{1}{200}\right)\)
\(\Rightarrow3.\frac{199}{200}=\frac{597}{200}\)

A=\(\frac{3.3}{8.11}\)+\(\frac{3.3}{11.14}\)+\(\frac{3.3}{14.17}\)+........+\(\frac{3.3}{197.200}\)
A=3\(\frac{3}{8.11}\)+3\(\frac{3}{11.14}\)+3\(\frac{3}{14.17}\)+............+3\(\frac{3}{197.200}\)
A=3.(\(\frac{3}{8.11}\)+\(\frac{3}{11.14}\)+\(\frac{3}{14.17}\)+..............+\(\frac{3}{197.200}\))
A=3.(\(\frac{1}{8}\)-\(\frac{1}{11}\)+\(\frac{1}{11}\)-\(\frac{1}{14}\)+\(\frac{1}{14}\)-\(\frac{1}{17}\)+.........+\(\frac{1}{197}\)-\(\frac{1}{200}\))
A=3.(\(\frac{1}{8}\)-\(\frac{1}{200}\))
A=3.(\(\frac{50}{400}\)-\(\frac{2}{200}\))
A=3.\(\frac{48}{400}\)
A=3.\(\frac{3}{25}\)
A=\(\frac{9}{25}\)

\(32\left(\frac{1}{8.11}+\frac{1}{11.14}+\frac{1}{14.17}+...+\frac{1}{197.200}\right)-x=\frac{1}{2}\)
\(\frac{32}{3}\left(\frac{3}{8.11}+\frac{3}{11.14}+\frac{3}{14.17}+....+\frac{3}{197.200}\right)-x=\frac{1}{2}\)
\(\frac{32}{3}\left(\frac{1}{8}-\frac{1}{11}+\frac{1}{11}-\frac{1}{14}+\frac{1}{14}-\frac{1}{17}+...+\frac{1}{197}-\frac{1}{200}\right)-x=\frac{1}{2}\)
\(\frac{32}{3}\left(\frac{1}{8}-\frac{1}{200}\right)-x=\frac{1}{2}\)
x=0.78

\(B=\frac{3^2}{8.11}+\frac{3^2}{11.14}+...+\frac{3^2}{197.200}\)
\(B=3.\left(\frac{1}{8.11}+\frac{1}{11.14}+...+\frac{1}{197.200}\right)\)
\(B=3.\left(\frac{1}{8}-\frac{1}{11}+\frac{1}{11}-\frac{1}{14}+...+\frac{1}{197}-\frac{1}{200}\right)\)
\(B=3.\left(\frac{1}{8}-\frac{1}{200}\right)\)
\(B=3.\frac{3}{25}\)
\(\Rightarrow B=\frac{9}{25}\)
\(B=\frac{3^2}{8.11}+\frac{3^2}{11.14}+...+\frac{3^2}{197.200}.\)
\(=3\left(\frac{3}{8.11}+\frac{3}{11.14}+...+\frac{3}{197.200}\right)\)
\(=3\left(\frac{11-8}{8.11}+\frac{14-11}{11.14}+...+\frac{200-197}{197.200}\right)\)
\(=3\left(\frac{1}{8}-\frac{1}{11}+\frac{1}{11}-\frac{1}{14}+...+\frac{1}{197}-\frac{1}{200}\right)\)
\(=3\left(\frac{1}{8}-\frac{1}{200}\right)\)
\(=3\cdot\frac{3}{25}\)
\(=\frac{9}{25}\)

E =\(\frac{3.3}{8.11}+\frac{3.3}{11.14}+.........+\frac{3.3}{197.200}\)
E =3.(\(\frac{1}{8}-\frac{1}{11}+\frac{1}{11}-\frac{1}{14}+\frac{1}{14}+.....+\frac{1}{200}\))
E =3.(\(\frac{1}{8}-\frac{1}{200}\))
E =3.(\(\frac{25}{200}-\frac{1}{200}\))
E =3.\(\frac{24}{200}\)
E =3.\(\frac{3}{25}\)
E =\(\frac{3}{1}.\frac{3}{25}\)
E =\(\frac{9}{25}\)

\(H=\frac{3^2}{2.5}+\frac{3^2}{5.8}+\frac{3^2}{8.11}+\frac{3^2}{11.14}+...+\frac{3^2}{197.200}=3.\left(\frac{3}{2.5}+\frac{3}{5.8}+...+\frac{3}{197.200}\right)=3.\left(\frac{1}{2}-\frac{1}{5}+\frac{1}{5}-\frac{1}{8}+...+\frac{1}{197}-\frac{1}{200}\right)=3\cdot\left(\frac{1}{2}-\frac{1}{200}\right)==\frac{297}{200}\)

\(\dfrac{3^2}{8.11}+\dfrac{3^2}{11.14}+...+\dfrac{3^2}{197.200}\)
=\(3.\left(\dfrac{3}{8.11}+\dfrac{3}{11.14}+...+\dfrac{3}{197.200}\right)\)
=\(3.\left(\dfrac{1}{8}-\dfrac{1}{11}+\dfrac{1}{11}-\dfrac{1}{14}+...+\dfrac{1}{197}-\dfrac{1}{200}\right)\)
=\(3.\left(\dfrac{1}{8}-\dfrac{1}{200}\right)\)
=\(3.\dfrac{3}{25}=\dfrac{9}{25}\)
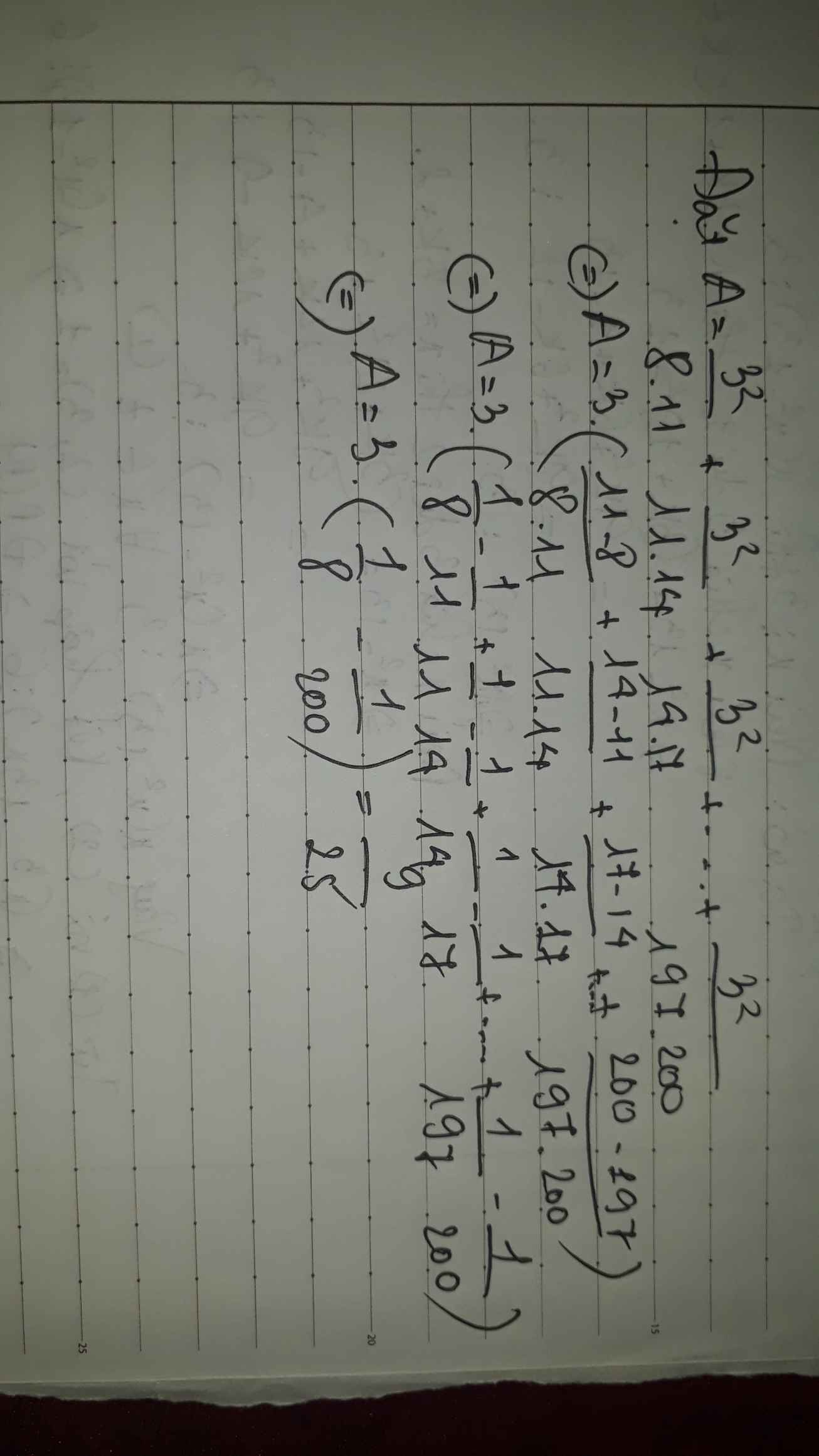
Đặt \(A=\frac{3^2}{8.11}+\frac{3^2}{11.14}+\frac{3^2}{14.17}+...+\frac{3^2}{197.200}\)
\(\Leftrightarrow A=\frac{9}{8.11}+\frac{9}{11.14}+\frac{9}{14.17}+...+\frac{9}{197.200}\)
\(\Leftrightarrow\frac{1}{3}A=\frac{3}{8.11}+\frac{3}{11.14}+\frac{3}{14.17}+...+\frac{3}{197.200}\)
\(\Leftrightarrow\frac{1}{3}A=\frac{1}{8}-\frac{1}{11}+\frac{1}{11}-\frac{1}{14}+\frac{1}{14}-\frac{2}{17}+...+\frac{1}{197}-\frac{1}{200}\)b
\(\Leftrightarrow\frac{1}{3}A=\frac{1}{8}-\frac{1}{200}\)
\(\Leftrightarrow\frac{1}{3}A=\frac{24}{200}\)
\(\Leftrightarrow A=\frac{24}{200}\times3\)
\(\Leftrightarrow A=\frac{72}{200}=\frac{9}{25}\)
Thank