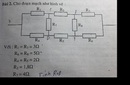
Tính điện trở tương đương của đoạn mạch sau đây.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
6 tháng 8 2018
Biểu thức xác định điện trở tương đương của đoạn mạch có hai điện trở R1, R2 mắc song song: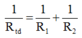 
→ Đáp án A
VT
29 tháng 4 2017
Ta có: Điện trở tương đương của đoạn mạch nối tiếp bằng tổng các điện trở hợp thành: Rtd = R1 + R2
Đáp án: C
VT
31 tháng 10 2017
Ta có:
Nghịch đảo điện trở tương đương của đoạn mạch song song bằng tổng các nghịch đảo điện trở các đoạn mạch rẽ: 1 R t d = 1 R 1 + 1 R 2
Đáp án: A
N
15 tháng 10 2021
Điện trở tương đương: \(R=\dfrac{\left(R1+R2\right)R3}{R1+R2+R3}=\dfrac{\left(15+25\right)10}{15+25+10}=8\Omega\)
\(U=U12=U3=12V\)(R12//R3)
\(I=U:R=12:8=1,5A\)
\(I3=U3:R3=12:10=1,2A\)
\(R1ntR2\Rightarrow I12=I1=I2\)
Mà: \(I12=I-I3=1,5-1,2=0,3A\)
\(\Rightarrow I12=I1=I2=0,3A\)
15 tháng 8 2021
R1//R2
a, =>\(Rtd=\dfrac{R1R2}{R1+R2}=\dfrac{20.20}{20+20}=10\left(ôm\right)\)
b,R1//R2//R3
\(=>\dfrac{1}{Rtd}=\dfrac{1}{R1}+\dfrac{1}{R2}+\dfrac{1}{R3}=\dfrac{1}{20}+\dfrac{1}{20}+\dfrac{1}{15}=>Rtd=6\left(ôm\right)\)c,
=>U1=U2=U3=30V
\(=>I1=\dfrac{U1}{R1}=\dfrac{30}{20}=1,5A,=>I2=\dfrac{U2}{R2}=1,5A\)
\(=>I3=\dfrac{U3}{R3}=2A\)
\(=>Im=\dfrac{U}{Rtd}=\dfrac{30}{6}=5A\)
VT
8 tháng 4 2017
a) Vì mạch mắc nối tiếp nên điện trở tương đương của đoạn mạch là:
RAB = R1 + R2 = 20 + 20 = 2.20 = 40Ω
b) Theo hình, điện trở R3 được mắc nối tiếp với R2 nên khi đó mạch điện mới gồm 3 điện trở mắc nối tiếp. Do đó, điện trở tương đương mới của đoạn mạch là:
RAC = R1 + R2 + R3 = RAB + R3 = 40 + 20 = 60 Ω
So sánh: RAC > R1, RAC > R2, RAC > R3
29 tháng 10 2023
\(a.R_{tđ}=R_1+R_2=4+6=10\Omega\\ b.R_{tđ}'=R_1+\dfrac{R_2.R_3}{R_2+R_3}=4+\dfrac{6.12}{6+12}=8\Omega\\ I=\dfrac{U_{AB}}{R_{tđ}'}=\dfrac{18}{8}=2,25A\\ Vì.R_1ntR_{23}\\ \Rightarrow I=I_1=I_{23}=2,25A\\ U_1=I_1.R_1=4.2,25=9V\\ U_{23}=U_{AB}-U_1=18-9=9V\\ Vì.R_2//R_3\Rightarrow U_{23}=U_2=U_3=9V\\ I_3=\dfrac{U_3}{R_3}=\dfrac{9}{12}=0,75A\)
Ta chuyển hai đầu của mạch cầu thành hai mạch sao, ta có:
- Đối với điện trở \(R_1;R_4;R_7\)
\(R_{14}=\frac{R_1.R_4}{R_1+R_4+R_7}=\frac{3.2}{3+2+4}=\frac{2}{3}\Omega\)
\(R_{17}=\frac{R_1.R_7}{R_1+R_4+R_7}=\frac{3.4}{3+2+4}=\frac{4}{3}\Omega\)
\(R_{47}=\frac{R_4.R_7}{R_1+R_4+R_7}=\frac{2.4}{3+2+4}=\frac{8}{9}\Omega\)
- Đối với điện trở \(R_3;R_6;R_8\)
\(R_{36}=\frac{R_3.R_6}{R_3+R_6+R_8}=\frac{3.5}{3+5+5}=\frac{15}{13}\Omega\)
\(R_{38}=\frac{R_3.R_8}{R_3+R_6+R_8}=\frac{3.5}{3+5+5}=\frac{15}{13}\Omega\)
\(R_{68}=\frac{R_6.R_8}{R_3+R_6+R_8}=\frac{5.5}{3+5+5}=\frac{25}{13}\Omega\)
Có đoạn mạch lúc này là: \(\left\{R_{14}nt[\left(R_{17}ntR_2ntR_{38}\right)//\left(R_{47}ntR_5ntR_{56}\right)]ntR_{36}\right\}\)
Điện trở tương đương của đoạn mạch này là:
\(R_{tđ}=R_{14}+\frac{\left(R_{17}+R_2+R_{38}\right)\left(R_{47}+R_5+R_{68}\right)}{R_{17}+R_2+R_{38}+R_{47}+R_5+R_{68}}+R_{36}\Leftrightarrow R_{tđ}=2+\frac{\left(\frac{4}{3}+1,8+\frac{15}{13}\right)\left(\frac{8}{9}+2+\frac{25}{13}\right)}{\frac{4}{3}+1,8+\frac{15}{13}+\frac{8}{9}+2+\frac{25}{13}}+\frac{15}{13}=4,087\Omega\)