
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vào C ra P
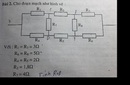
Cấu trúc mạch điện là (R2ntR6)//(R1ntR8)//(R3ntR7)
mà mỗi điện trở có R=30(ôm)
1/Rtương đương=1/(R2+R6) +1/(R1+R8) +1/(R3+R7)=1/20
suy ra Rtương đương =20(ôm)

A, Rtđ = 6 ôm
Iab= 3 = I1 = I2 vì R1 nt R2
a, R1 nt (R2 // R3 )
Rtđ = R1 + [R2×R3÷(R2+R3)]= 4
b, I =Uab÷Rtđ = 18 ÷4 =4.5 = I1 =I23
U1 =I1 × R1 =3 ×4 =12
U23 = Uab - U1 = 18 - 12 = 6
Vì R2 // R3 => U23 = U2 = U3 = 6
R1 nt R2, ta có:
A. Điện trở tương đương :
Rtđ = R1 + R2 = 4 + 6 = 10 ( Ω )
Cường độ dòng điện chạy qua toàn mạch:
Iab = \(\dfrac{\text{Uab}}{\text{Rtđ}}\) = \(\dfrac{\text{18}}{\text{10}}\) = 1.8 ( A )
Iab = I1 = I2 = 1.8 A
B.
a.


a) mạch ((R3//R4)ntR2)//R1=>Rtđ=7,5\(\Omega\)
b) R342//R1=>U324=U1=U
=>I1=\(\dfrac{U}{15}A\)
Vỉ R34ntR2=>I34=I2=\(\dfrac{U}{15}A\)
Vì R3//R4=>U3=U4=U34=I34.R34=\(\dfrac{U}{15}.5=\dfrac{U}{3}V\)=>I3=\(\dfrac{U3}{R3}=\dfrac{U}{3.10}\)
=>I4=\(\dfrac{U4}{10}=\dfrac{U}{3.10}A\)
ta có Ia=I1+I3=3A=>\(\dfrac{U}{15}+\dfrac{U}{30}=3=>U=30V\)
Thay U=30V tính được I1=2A;I2=2A;I4=1A;I3=1A
Vậy........

















 tick cho mình nha !!!
tick cho mình nha !!!
Ta chuyển hai đầu của mạch cầu thành hai mạch sao, ta có:
- Đối với điện trở \(R_1;R_4;R_7\)
\(R_{14}=\frac{R_1.R_4}{R_1+R_4+R_7}=\frac{3.2}{3+2+4}=\frac{2}{3}\Omega\)
\(R_{17}=\frac{R_1.R_7}{R_1+R_4+R_7}=\frac{3.4}{3+2+4}=\frac{4}{3}\Omega\)
\(R_{47}=\frac{R_4.R_7}{R_1+R_4+R_7}=\frac{2.4}{3+2+4}=\frac{8}{9}\Omega\)
- Đối với điện trở \(R_3;R_6;R_8\)
\(R_{36}=\frac{R_3.R_6}{R_3+R_6+R_8}=\frac{3.5}{3+5+5}=\frac{15}{13}\Omega\)
\(R_{38}=\frac{R_3.R_8}{R_3+R_6+R_8}=\frac{3.5}{3+5+5}=\frac{15}{13}\Omega\)
\(R_{68}=\frac{R_6.R_8}{R_3+R_6+R_8}=\frac{5.5}{3+5+5}=\frac{25}{13}\Omega\)
Có đoạn mạch lúc này là: \(\left\{R_{14}nt[\left(R_{17}ntR_2ntR_{38}\right)//\left(R_{47}ntR_5ntR_{56}\right)]ntR_{36}\right\}\)
Điện trở tương đương của đoạn mạch này là:
\(R_{tđ}=R_{14}+\frac{\left(R_{17}+R_2+R_{38}\right)\left(R_{47}+R_5+R_{68}\right)}{R_{17}+R_2+R_{38}+R_{47}+R_5+R_{68}}+R_{36}\Leftrightarrow R_{tđ}=2+\frac{\left(\frac{4}{3}+1,8+\frac{15}{13}\right)\left(\frac{8}{9}+2+\frac{25}{13}\right)}{\frac{4}{3}+1,8+\frac{15}{13}+\frac{8}{9}+2+\frac{25}{13}}+\frac{15}{13}=4,087\Omega\)