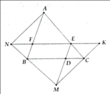
Cho tam giác ABC, đường thẳng song song BC cắt AB, AC tại D và E. Vẽ đường thẳng a đi qua A và song song với BC. Đường thẳng a cắt BE và CD lần lượt tại G và K. Chứng minh A là trung điểm KG
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
3 tháng 2 2020
+ Xét \(\Delta ABC\)có :
\(DE//BC\left(gt\right)\)
\(\Rightarrow\frac{AD}{DB}=\frac{AE}{EC}\)( định lí Ta - lét ) (1)
+ Xét \(\Delta DBC\)có :
\(AK//BC\left(gt\right)\)
\(\Rightarrow\frac{AK}{BC}=\frac{AD}{DB}\)( định lí Ta - lét ) (2)
+ Xét \(\Delta BEC\)có:
\(AG//BC\left(gt\right)\)
\(\Rightarrow\frac{AG}{BC}=\frac{AE}{EC}\)( định lí Ta - lét ) (3)
Từ (1) , (2) và (3) \(\Rightarrow\frac{AK}{BC}=\frac{AG}{BC}\)
\(\Rightarrow AK=AG\)
\(\Rightarrow A\)là trung điểm của KG (đpcm)
Chúc bạn học tốt !!!
VM
11 tháng 1 2020
Sửa lại là CM: A là trung điểm của KG nhé.
+ Xét \(\Delta ABC\) có:
\(DE\) // \(BC\left(gt\right)\)
=> \(\frac{AD}{DB}=\frac{AE}{EC}\) (định lí Ta - lét) (1).
+ Xét \(\Delta DBC\) có:
\(AK\) // \(BC\left(gt\right)\)
=> \(\frac{AK}{BC}=\frac{AD}{DB}\) (định lí Ta - lét) (2).
+ Xét \(\Delta BEC\) có:
\(AG\) // \(BC\left(gt\right)\)
=> \(\frac{AG}{BC}=\frac{AE}{EC}\) (định lí Ta - lét) (3).
Từ (1), (2) và (3) \(\Rightarrow\frac{AK}{BC}=\frac{AG}{BC}.\)
=> \(AK=AG.\)
=> A là trung điểm của \(KG\left(đpcm\right).\)
Chúc bạn học tốt!
