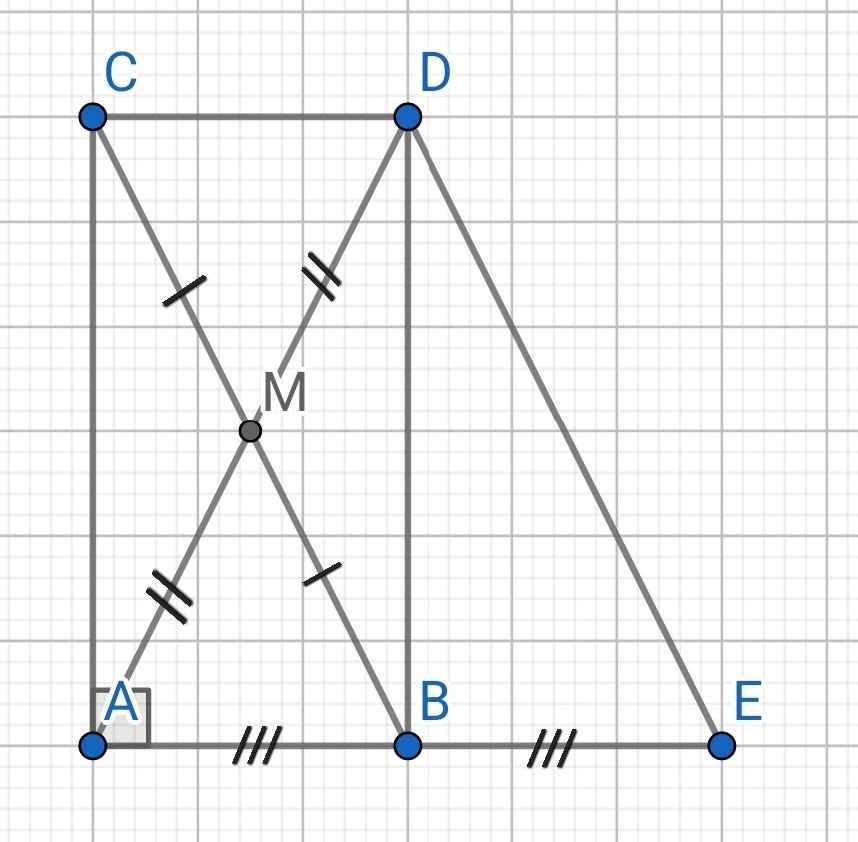
Cho tam giác nhọn ABC có AC < AB. Kẻ trung tuyến AM, trên tia AM lấy điểm D sao cho MA = MD
a, Chứng minh tứ giác ABDC là hình bình hành
b, Gọi E là điểm đối xứng của A của đường thẳng BC. Gọi H là giao điểm của AE và BC. Chứng minh AE ⊥ ED
c, Chứng minh tứ giác BCDE là hình thang cân. Cho AE = 12cm, MC = 2,5cm. Tính diện tích tam giác...
Đọc tiếp
Cho tam giác nhọn ABC có AC < AB. Kẻ trung tuyến AM, trên tia AM lấy điểm D sao cho MA = MD
a, Chứng minh tứ giác ABDC là hình bình hành
b, Gọi E là điểm đối xứng của A của đường thẳng BC. Gọi H là giao điểm của AE và BC. Chứng minh AE ⊥ ED
c, Chứng minh tứ giác BCDE là hình thang cân. Cho AE = 12cm, MC = 2,5cm. Tính diện tích tam giác ABC
ABC vuông tại A (AB < AC), trung tuyến AM, đường cao AH. Trên tia đối của tia MA lấy điểm D sao cho MD = MA.
AB tại E, HF 
a) Xét tứ giác $ABDC$ có :
$AM = MD ; BM = MC$
$\to$ Tứ giác $ABDC$ là hình bình hành
a: Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
nên ABDC là hình bình hành
b E đối xứng A qua BC
=>BC vuông góc AE tại H và H là trung điểm của AE
Xét ΔAED có AH/AE=AM/AD
nên HM//ED
=>ED vuông góc với AE
c: A đối xứng E qua BC
nên CA=CE=BD
Xét tứ giác BEDC có
BC//DE
BD=EC
=>BEDC là hình thang cân
AE=12cm =>AH=6cm
MC=2,5cm
=>BC=5cm
\(S_{ABC}=\dfrac{1}{2}\cdot6\cdot5=3\cdot5=15\left(cm^2\right)\)