Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

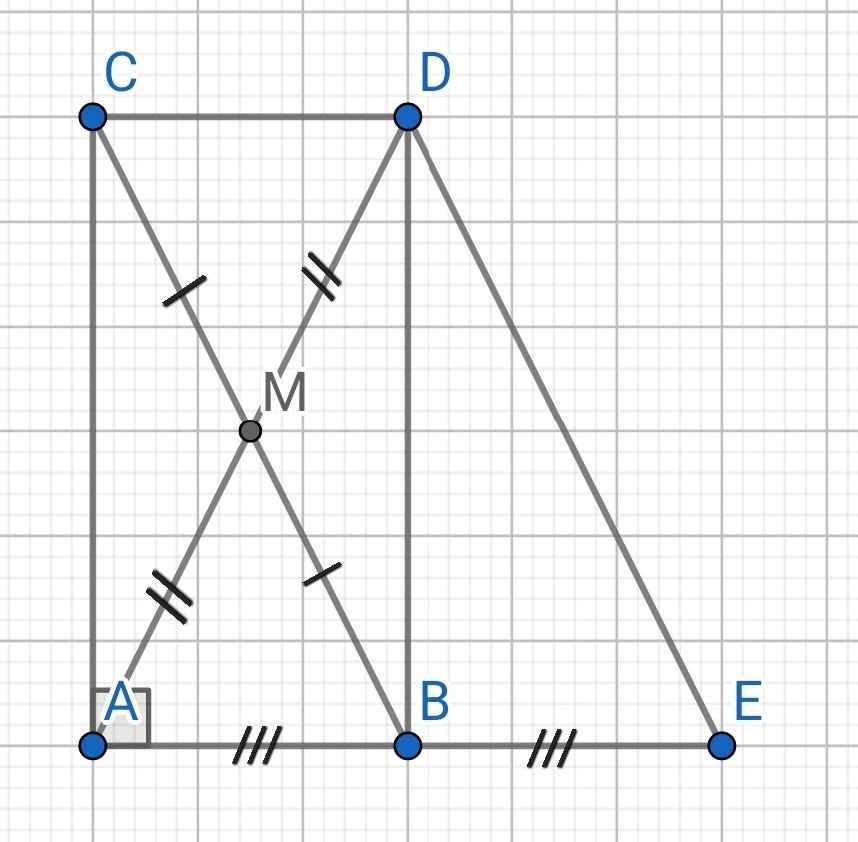
a: Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
nên ABDC là hình bình hành
b: E đối xứng A qua BC
nên BC vuông góc AE tại H và H là trung điểm của AE
Xét ΔAED có AH/AE=AM/AD
nên HM//ED
=>ED vuông góc với EA
c: A đối xứng E qua CB
nên CA=CE=BD
Xét tứ giác BCDE có
BC//DE
BD=CE
=>BCDE là hình thang cân

 a) Tứ giác ABDC có:
a) Tứ giác ABDC có:
M là trung điểm của BC (gt)
M là trung điểm của AD (gt)
⇒ ABDC là hình bình hành
Mà ∠BAC = 90⁰ (∆ABC vuông tại A)
⇒ ABDC là hình chữ nhật
b) Do ABDC là hình chữ nhật (cmt)
⇒ CD = AB (1)
Do B là trung điểm của AE (gt)
⇒ BE = AB = AE : 2 (2)
Từ (1) và (2) ⇒ CD = BE
Do ABDC là hình chữ nhật (cmt)
⇒ CD // AB
⇒ CD // BE
Tứ giác BEDC có:
CD // BE (cmt)
CD = BE (cmt)
⇒ BEDC là hình bình hành
c) Do ABDC là hình chữ nhật (cmt)
⇒ AC // BD
Do đó AC, BD, EK đồng quy là vô lý
Em xem lại đề nhé!

a) Xét ∆CMA và ∆BMD:
Góc CMA= góc BMD (đối đỉnh)
MA=MD (gt)
MC=MB (M là trung điểm BC)
=> ∆CMA=∆BMD(c.g.c)
=> góc CAM = góc BDM và CA=DB
Mà 2 góc CAM và góc BDM nằm ở vị trí so lo trong nên CA//DB
=> CABD là hình bình hành
Lại có góc CAB = 90 độ (gt)
=> ACDB là hình chữ nhật
b) Vì E là điểm đối xứng của C qua A nên EAB=90độ=DBA
Mà 2 góc này ở bị trí so le trong nên AE//DB
Lại có AE=BD(=CA)
=> AEBD là hình bình hành

a: Xét tứ giác AEBM có
D là trung điểm của AB
D là trung điểm của ME
Do đó:AEBM là hình bình hành
Suy ra: AM//BE và AM=BE
=>AM//CE và AM=CE
hay ACEM là hình bình hành
b: Xét hình bình hành AMBE có \(\widehat{AEB}=90^0\)
nên AMBE là hình chữ nhật
c: BC=12cm
=>BE=6cm
\(S_{AEB}=\dfrac{BE\cdot AE}{2}=\dfrac{6\cdot8}{2}=24\left(cm^2\right)\)

a) Xét tứ giác AMBE có
D là trung điểm của đường chéo AB(gt)
D là trung điểm của đường chéo ME(M và E đối xứng nhau qua D)Do đó: AMBE là hình bình hành(Dấu hiệu nhận biết hình bình hành)
Ta có: AMBE là hình bình hành(cmt)
nên AM//BE và AM=BE(Hai cạnh đối của hình bình hành AMBE)
mà \(C\in EB\) và EB=EC(E là trung điểm của BC)
nên AM//CE và AM=CE
Xét tứ giác AMEC có
AM//CE(cmt)
AM=CE(cmt)
Do đó: AMEC là hình bình hành(Dấu hiệu nhận biết hình bình hành)
b) Ta có: ΔABC cân tại A(gt)
mà AE là đường trung tuyến ứng với cạnh đáy BC(E là trung điểm của BC)
nên AE là đường cao ứng với cạnh BC(Định lí tam giác cân)
⇔AE⊥BC
hay \(\widehat{AEB}=90^0\)
Xét hình bình hành AMBE có \(\widehat{AEB}=90^0\)(cmt)
nên AMBE là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)
c) Ta có: E là trung điểm của BC(gt)
nên \(BE=\dfrac{BC}{2}=\dfrac{12}{2}=6\left(cm\right)\)
Ta có: ΔABE vuông tại E(\(\widehat{AEB}=90^0\))
nên \(S_{ABE}=\dfrac{AE\cdot EB}{2}=\dfrac{6\cdot8}{2}=24\left(cm^2\right)\)


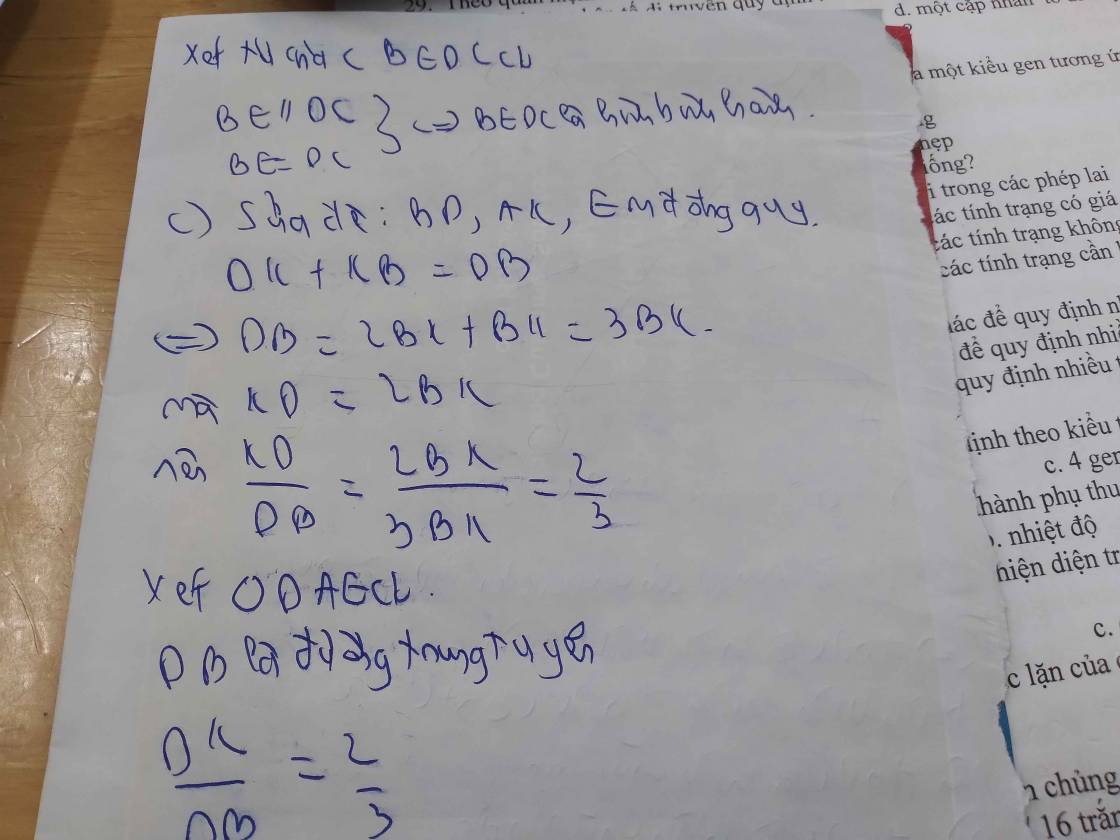

a) Xét tứ giác $ABDC$ có :
$AM = MD ; BM = MC$
$\to$ Tứ giác $ABDC$ là hình bình hành
a: Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
nên ABDC là hình bình hành
b E đối xứng A qua BC
=>BC vuông góc AE tại H và H là trung điểm của AE
Xét ΔAED có AH/AE=AM/AD
nên HM//ED
=>ED vuông góc với AE
c: A đối xứng E qua BC
nên CA=CE=BD
Xét tứ giác BEDC có
BC//DE
BD=EC
=>BEDC là hình thang cân
AE=12cm =>AH=6cm
MC=2,5cm
=>BC=5cm
\(S_{ABC}=\dfrac{1}{2}\cdot6\cdot5=3\cdot5=15\left(cm^2\right)\)