Cho tam giác ABC vuông tại A,đường cao AH.Trên BC lấy điểm D sao cho BD=BA.chứng minh rằng:AB+AC<BC+AH,DH<DC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 5 2022
a: Xét ΔBAD có BA=BD
nên ΔBAD cân tại B
hay \(\widehat{BAD}=\widehat{BDA}\)
b: Ta có: \(\widehat{CAD}+\widehat{BAD}=90^0\)
\(\widehat{HAD}+\widehat{BDA}=90^0\)
mà \(\widehat{BAD}=\widehat{BDA}\)
nên \(\widehat{CAD}=\widehat{HAD}\)
hay AD là tia phân giác của góc HAC
YP
11 tháng 5 2022
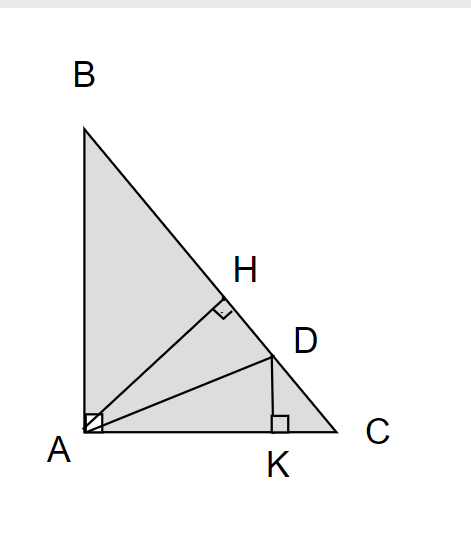
c, Ta có: Góc CAD= góc HAD
hay góc KAD= góc HAD
Xét △ AHD và △AKD có:
AD chung
Góc AHD= góc AKD= 90 độ
Góc KAD= góc HAD
=> △AHD= △AKD (cạnh huyền- góc nhọn)
=> AH= AK (2 cạnh tương ứng)
7 tháng 4 2023
Gọi giao của CD với AB là G
góc HAB=góc HCD
=>góc GCB+góc GBC=90 độ
=>CD vuông góc AB
Xét ΔABC có
CD,AH là đường cao
CD căt AH tại D
=>D là trực tam
=>BD vuông gócAC
2 tháng 7 2023
Xét ΔBHE vuông tại H và ΔBDC vuông tại D có
góc DBC chung
=>ΔBHE đồng dạng với ΔBDC
=>BH/BD=BE/BC
=>BH*BC=BD*BE
Lấy K trên cạnh AC sao cho AK=AH.
+) Ta có: ^BAD = ^BAH + ^HAD = ^ACD + ^HAD = ^BDA = ^ACD + ^DAC => ^HAD = ^KAD
Do đó: \(\Delta\)AHD = \(\Delta\)AKD (c.g.c) => ^AHD = ^AKD => ^AKD = 900
=> \(\Delta\)DCK vuông tại K => CK < CD <=> AC - AK < BC - BD <=> AC - AH < BC - AB
<=> AB + AC < BC + AH (đpcm).
+) \(\Delta\)AHD = \(\Delta\)AKD (cmt) => DH = DK. Mà DK < DC do \(\Delta\)DCK vuông K (cmt) => DH < DC (đpcm).
Nguyễn Tất Đạt:Thanks anh very nhiều ah!