hai vòi nước cùng chảy vào một bể nước cạn thì sau \(4\frac{4}{5}\)giờ thì đầy bể. Nếu lúc đầu chỉ mở vòi 1 , sau 9 giờ mới mở vòi vòi hai thì sau\(\frac{6}{5}\)giờ bể đầy. Nếu ngay từ đầu chỉ mở vòi hai thì mấy giờ bể đầy?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
20 tháng 1 2019
b tham khảo bài 4 tương tự trong này nhé https://cunghocvui.com/danh-muc/vat-ly-lop-9
CM
22 tháng 11 2017
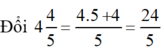
Cách 1.
Gọi thời gian để vòi thứ nhất, vòi thứ 2 chảy 1 mình đầy bể là x (h), y (h).
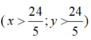
+ Một giờ vòi thứ nhất chảy được :1/x ( bể )
Một giờ vòi thứ hai chảy được :1/y ( bể )
+ Hai vòi nước cùng chảy vào một bể nước cạn (không có nước) thì sau 4 4 5 = 24 5 giờ đầy bể.
=> Một giờ cả hai vòi chảy được :
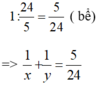
* Nếu ban đầu mở vòi 1 và 9 giờ sau mở thêm vòi 2 thì sau 6/5 (h) đầy bể. Khi đó, thời gian vòi 1 chảy là : 9 + 6 5 = 51 5 ( h ) .
Thời gian vòi 2 chảy là 6/5 (h)
Vậy nếu ngay từ đầu chỉ mở vòi 2 thì sau 8 giờ sẽ đầy bể.
Cách 2.
Gọi lượng nước vòi thứ nhất và vòi thứ hai chảy một mình trong 1 giờ lần lượt là x (bể) và y (bể).
Điều kiện 0 < x, y < 1.
+ Cả hai vòi cùng chảy trong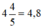 
giờ đầy 1 bể nên ta có phương trình: 4,8x + 4,8y = 1.
+ Nếu mở vòi thứ nhất trong 9 giờ thì chảy được 9x (bể)
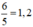giờ sau mở thêm vòi thứ hai thì chảy thêm được: 1,2 (x + y) (bể)
Khi đó bể đầy nên ta có phương trình: 9x + 1,2(x + y) = 1.
Ta có hệ phương trình
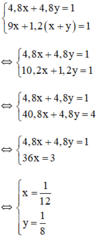
⇒ một giờ vòi hai chảy một mình được 1/8 bể
Vậy nếu ngay từ đầu chỉ mở vòi thứ hai thì sau 8 giờ sẽ đầy bể.
Kiến thức áp dụng
Giải bài toán bằng cách lập hệ phương trình :
Bước 1 : Lập hệ phương trình
- Chọn các ẩn số và đặt điều kiện thích hợp
- Biểu diễn các đại lượng chưa biết và đã biết theo ẩn
- Lập các phương trình biểu thị mối quan hệ giữa các đại lượng theo đề bài.
- Từ các phương trình vừa lập rút ra được hệ phương trình.
Bước 2 : Giải hệ phương trình (thường sử dụng phương pháp thế hoặc cộng đại số).
Bước 3 : Đối chiếu nghiệm với điều kiện và kết luận.
HT
Hoàng Thị Thu Huyền
Manager
10 tháng 4 2017
Gọi x, y lần lượt là thời gian để hai vòi chảy một mình thì đầy bể \(\left(x,y>4\dfrac{4}{5};giờ\right)\)
Đổi \(4\dfrac{4}{5}\left(h\right)=\dfrac{24}{5}\left(h\right)\)
Một giờ vòi 1 chảy được \(\dfrac{1}{x}\) bể, vòi 2 chảy được \(\dfrac{1}{y}\). Trong một giờ cả hai vòi chảy được \(1:\dfrac{24}{5}=\dfrac{5}{24}\) (bể)
Vậy ta có phương trình: \(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{5}{24}\)
Trong \(\dfrac{6}{5}\left(h\right)\) hai vòi chảy được là: \(\dfrac{6}{5}\left(\dfrac{1}{x}+\dfrac{1}{y}\right)\) (bể)
Theo giả thiết ta lại có phương trình: \(\dfrac{9}{x}+\dfrac{6}{5}\left(\dfrac{1}{x}+\dfrac{1}{y}\right)=1\)
Vậy ta có hệ: \(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{5}{24}\\\dfrac{51}{5x}+\dfrac{6}{5y}=1\end{matrix}\right.\)
Đặt \(\dfrac{1}{x}=u;\dfrac{1}{y}=v\Rightarrow\left\{{}\begin{matrix}u+v=\dfrac{5}{24}\\\dfrac{51}{5}u+\dfrac{6}{5}v=1\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}u=\dfrac{1}{12}\\v=\dfrac{1}{8}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{1}{x}=\dfrac{1}{12}\\\dfrac{1}{y}=\dfrac{1}{8}\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=12\\y=8\end{matrix}\right.\left(tm\right)\)
Vậy nếu ngay từ đầu chỉ mở vòi hai thì sau 8 giờ sẽ đầy bể.
HB
9 tháng 4 2017
Gọi x (giờ) là thời gian để vòi thứ nhất chảy đầy bể (x > 0).
y (giờ) là thời gian để vòi thứ hai chảy đầy bể (y > 0).
Trong 1 giờ vòi thứ nhất chảy được bể, vòi thứ hai chảy được
bể.
Cả hai vòi cùng chảy thì bể đầy sau giờ =
giờ nên trong 1 giờ cả hai vòi cùng chảy được
bể.
Ta được: +
=
Trong 9 giờ cả hai vòi chảy được bể.
Trong giờ cả hai vòi chảy được
(
+
) bể.
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
14 tháng 10 2023
Phân số chỉ lượng nước vòi 1 chảy trong 1 giờ là
\(1:3=\dfrac{1}{3}\) bể
Phân số chỉ lượng nước vòi 2 chảy trong 1 giờ là
\(1:4=\dfrac{1}{4}\) bể
Phân số chỉ lượng nước vòi 3 chảy trong 1 giờ là
\(1:6=\dfrac{1}{6}\) bể
Phân số chỉ lượng nước 3 vòi cùng chảy trong 1 giờ là
\(\dfrac{1}{3}+\dfrac{1}{4}-\dfrac{1}{6}=\dfrac{5}{12}\) bể
Phân số chỉ lượng nước 3 vòi cùng chảy đến khi đầy bể khi lượng nước có 3/5 bể là
\(1-\dfrac{3}{5}=\dfrac{2}{5}\) bể
Thời gian đầy bể là
\(\dfrac{2}{5}:\dfrac{5}{12}=\dfrac{24}{25}\) giờ
19 tháng 2 2023
Gọi thời gian chảy riêng của vòi 1 và vòi 2 lần lượt là a,b
Theo đề, ta có hệ:
1/a+1/b=1/6 và 10/a+4/b=1
=>a=18; b=9
XT
24 tháng 6 2015
bai 6:
P/S chi so phan be voi thu nhat chay trong 1 gio la:
1:5=1/5(be)
P/S chi so phan be voi thu hai chay trong 1 gio la:
1:7=1/7(be)
P/S chi so phan be trong 1 gio ca hai voi cung chay la:
1/5+1/7=12/35(be)
neu hai voi cung chay thi sau:
1:12/35=2gio 55 phut
minh chi lam vay thoi chu lam het thi lau lam
MP
30 tháng 12 2015
Đầu bài ở dạng vòi nước chảy vào bể thì ta tạm chấp nhập logic lượng nước chảy vào là hằng số (hằng số trên 1 đơn vị thời gian).
Trong thực tế vòi nước tháo ra: áp xuất trong bể càng lớn (lượng nước trong bể càng nhiều) thì lượng nước tháo ra càng nhiều. do đó cần bổ xung thêm đầu bài là lượng nước tháo ra cũng là hằng số (hằng số trên 1 đơn vị thời gian)
26 tháng 10 2021
1 giờ vòi 1 chảy được \(\dfrac{1}{3}\left(bể\right)\)
1 giờ vòi 2 chảy được \(\dfrac{1}{4}\left(bể\right)\)
1 giờ vòi 3 tháo được \(\dfrac{1}{6}\left(bể\right)\)
Do đó 1 giờ cả 3 vòi cùng mở thì chảy được \(\dfrac{1}{3}+\dfrac{1}{4}-\dfrac{1}{6}=\dfrac{5}{12}\left(bể\right)\)
Vậy sau \(1:\dfrac{5}{12}=\dfrac{12}{5}\left(giờ\right)\) thì đầy bể
15 tháng 10 2022
Nếu vòi 1 chảy một mình thì được số phần bể là :
1 : 3 = 1313 (bể)
Nếu vòi 2 chảy một mình thì được số phần bể là :
1 : 4 = 1414(bể)
Nếu vòi 3 chảy một mình thì chảy được số phần bể là :
1 : 6 = 1616(bể)
Nếu cả ba vòi cùng chảy thì được số phần bể là :
1313 + 1414 - 1616 = 512512(bể)
Nếu bể cạn thì mở cả ba vòi thì sau số giờ sẽ đầy bể là :
1 : 512512 = 125125 (giờ)
Đáp số : 125125 giờ
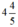
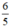
Gọi thời gian vòi 1 và vòi 2 chảy một mình đầy bể lần lượt là a,b
Theo đề, ta có:
\(\left\{{}\begin{matrix}\dfrac{1}{a}+\dfrac{1}{b}=1:\dfrac{24}{5}=\dfrac{5}{24}\\\dfrac{10.2}{a}+\dfrac{1.2}{b}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=12\\b=8\end{matrix}\right.\)