cho tam giác ABC trên BC lấy M bất kì . Trên AM lấy D bất kì . CMR: \(\dfrac{S_{ABD}}{S_{ACD}}=\dfrac{BM}{CM}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 9 2021
Đề bài của em bị sai
Hai tam giác BHD và BKC đồng dạng do chung góc \(\widehat{KBC}\) và \(\widehat{BDH}=\widehat{BCK}\) (cùng bằng \(\widehat{BAH}\))
Do đó tỉ số đồng dạng 2 tam giác là \(k=\dfrac{BD}{BC}\)
\(\Rightarrow\dfrac{S_{BDH}}{S_{BKC}}=k^2=\dfrac{BD^2}{BC^2}\)
Nếu đề bài đúng thì đồng nghĩa ta phải chứng minh:
\(\dfrac{BD^2}{BC^2}=\dfrac{cos^2\widehat{ABD}}{4}=\dfrac{\left(\dfrac{BD}{AB}\right)^2}{4}=\dfrac{BD^2}{4AB^2}\)
\(\Rightarrow BC^2=4AB^2\) nhưng điều này rõ ràng ko đúng (vì đề bài ko hề cho BC=2AB)
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 2 2022
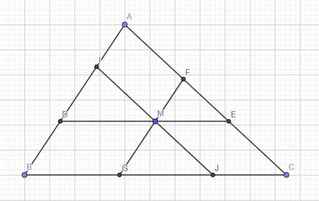
\(\left\{{}\begin{matrix}\widehat{MGJ}=\widehat{B}\left(\text{đồng vị}\right)\\\widehat{MJG}=\widehat{C}\left(\text{đồng vị}\right)\end{matrix}\right.\) \(\Rightarrow\Delta MGJ\sim\Delta ABC\) theo tỉ số \(k_1=\dfrac{GJ}{BC}\)
\(\Rightarrow S_{ABC}.k_1^2=S_{MGJ}\Rightarrow k_1=\sqrt{\dfrac{S_{MGJ}}{S_{ABC}}}=\dfrac{GJ}{BC}\) (1)
Tương tự: \(\dfrac{DM}{BC}=\sqrt{\dfrac{S_{IDM}}{S_{ABC}}}\), mà BDMG là hbh (2 cặp cạnh đối song song)
\(\Rightarrow DM=BG\Rightarrow\dfrac{BG}{BC}=\sqrt{\dfrac{S_{IDM}}{S_{ABC}}}\) (2)
Tương tự: \(\dfrac{CJ}{BC}=\sqrt{\dfrac{S_{FME}}{S_{ABC}}}\) (3)
Cộng vế (1);(2);(3) \(\Rightarrow\sqrt{\dfrac{S_{MGJ}}{S_{ABC}}}+\sqrt{\dfrac{S_{IDM}}{S_{ABC}}}+\sqrt{\dfrac{S_{FME}}{S_{ABC}}}=\dfrac{BG+GJ+JC}{BC}=1\)
\(\Rightarrow S_{ABC}=\left(\sqrt{S_{MGJ}}+\sqrt{S_{IDM}}+\sqrt{S_{FME}}\right)^2\le3\left(S_{MGJ}+S_{IDM}+S_{FME}\right)\)
Mà \(S_{MGJ}+S_{IDM}+S_{FME}=S_{ABC}-\left(S_{AIMF}+S_{BGMD}+S_{CEMJ}\right)\)
\(\Rightarrow S_{ABC}\le3\left[S_{ABC}-\left(S_{AIMF}+S_{BGMD}+S_{CEMJ}\right)\right]\)
\(\Rightarrow S_{AIMF}+S_{BGMD}+S_{CEMJ}\le\dfrac{2}{3}S_{ABC}\)
2 tháng 12 2023
Xét ΔCBE có AM//BE
nên \(\dfrac{AM}{BE}=\dfrac{CM}{CB}\)
Xét ΔBDC có AM//DC
nên \(\dfrac{AM}{DC}=\dfrac{BM}{BC}\)
\(\dfrac{AM}{BE}+\dfrac{AM}{DC}=\dfrac{BM}{BC}+\dfrac{CM}{BC}\)
=>\(AM\left(\dfrac{1}{BE}+\dfrac{1}{DC}\right)=\dfrac{BC}{BC}=1\)
=>\(\dfrac{1}{AM}=\dfrac{1}{BE}+\dfrac{1}{CD}\)
20 tháng 3 2023
a: BD/CD=AB/AC=1/2
b: Xét ΔAMB và ΔABC có
AM/AB=AB/AC
góc MAB=góc BAC
=>ΔAMB đồng dạng với ΔABC