Cho tam giác ABC.D là trung điểm của BC.Trên tia đối của tia DA lấy E sao cho DA=DE.
a/CMR:AB//EC
b/Kẻ AH và EK cùng vuông góc với BC(H thuộc BC, thuộc BC).CMR:AH=EK
c/Trên AC lấy M, trên BE lấy N sao cho AM=EN.CMR:M,N,D thẳng hàng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

CM: a) Xét t/giác ABD và t/giác ECD
có AD = DE (gt)
góc BDA = góc EDC (đối đỉnh)
BD = DC (gt)
=> t/giác ABD = t/giác ECD (c.g.c)
=> góc BAD = góc DEC (hai góc tương ứng)
Mà góc BAD và góc DEC ở vị trí so le trong
=> AB // EC (Đpcm)
b) Ta có : t/giác ABD = t/giác ECD (Cmt)
=> AB = EC (hai cạnh tương ứng)
=> góc B = góc DCE
Xét t/giác ABH và t/giác ECK
có góc BHA = góc CKE = 900 (gt)
AB = EC (cmt)
góc B =góc KCE (cmt)
=> t/giác ABH = t/giác ECK (cạnh huyền - góc nhọn)
c) tự làm

a: Xét tứ giác ABEC có
D là trung điểm chung của AE và BC
nên ABEC là hình bình hành
=>AC//BE và AB//CE
b: Xét ΔAHD vuông tại H và ΔEKD vuông tại K có
DA=DE
góc ADH=góc EDK
Do đo: ΔAHD=ΔEKD
=>AH=KE
c: Xét tứ giác AMEN có
AM//EN
AM=EN
Do đó: AMEN là hình bình hành
=>AE cắtMN tại trung điểm của mỗi đường
=>M,K,N thẳng hàng

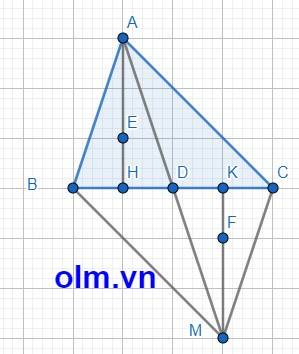
Xét tam giác ACD và tam giác MBD có:
AD = DM (gt)
BD = DC (gt)
\(\widehat{BDM}\) = \(\widehat{ADC}\) (hai góc đối đỉnh)
⇒ \(\Delta\)ACD = \(\Delta\) MBD (c-g-c)
Xét tứ giác ABMC có
AD = DM
BD = DC
⇒ tứ giác ABMC là hình bình hành vì tứ giác có hai đường chéo căt nhau tại trung điểm mỗi đường thì tứ giác đó là hình bình hành.
⇒ AC // BM
⇒ \(\widehat{ABM}\) = \(\widehat{MCA}\) (vì tứ giác ABMC là hình bình hành)
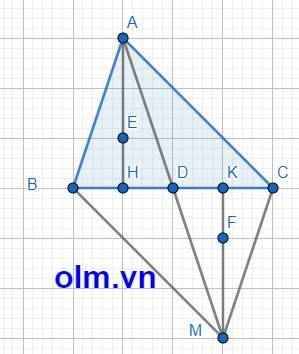
xét tam giác ACD và tam giác MBD có
AD=DM [ gt ]
BD=DC[ gt ]
BDM = ADC hai góc đối đỉnh
suy ra tam giác ACD= tam giác MBD [ c-g-c]
xét tứ giác ABMC có
AD = DM
BD=DC
suy ra tứ giác ABMC là hình bình hành vì tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường thì tứ giác đó là hình bình hành
suy ra ABM=MCA vì tứ giác ABMC là hình bình hành .

1.Ta có: AB = AC `=>` Tam giác ABC cân
Xét tam giác ABD và tam giác ACD, có:
AB = AC ( gt )
BD = CD ( gt )
AD: cạnh chung
Vậy tam giác ABD = tam giác ACD ( c.c.c )
Xét tam giác ABC có AB = AC `=>` Tam giác ABC cân
Mà AD là đường trung tuyến `=>` AD cũng là đường cao
`=>` AD vuông góc BC
2. Xét tam giác ADC và tam giác EDB, có:
BD = CD ( gt)
\(\widehat{BDE}=\widehat{ADC}\) ( đối đỉnh )
AD = ED ( gt )
Vậy tam giác ADC = tam giác EDB ( c.g.c )
`=>` \(\widehat{DAC}=\widehat{DEB}\)
`=>` AC // BE ( so le trong )
3. Xét tam giác AMD và tam giác AND, có:
AM = AN ( gt )
\(\widehat{MAD}=\widehat{NAD}\) (tam giác ABC cân, AD là đường cao cũng là phân giác )
AD: chung
Vậy tam giác AMD = tam giác AND ( c.g.c )
\(\Rightarrow\widehat{AMD}=\widehat{AND}=90^o\)
\(\Rightarrow DN\perp AC\) (1)
Ta có: \(DK\perp BE\) ( gt ) (2)
mà BE // AC (3)
(1);(2);(3) `=>` N,D,K thẳng hàng

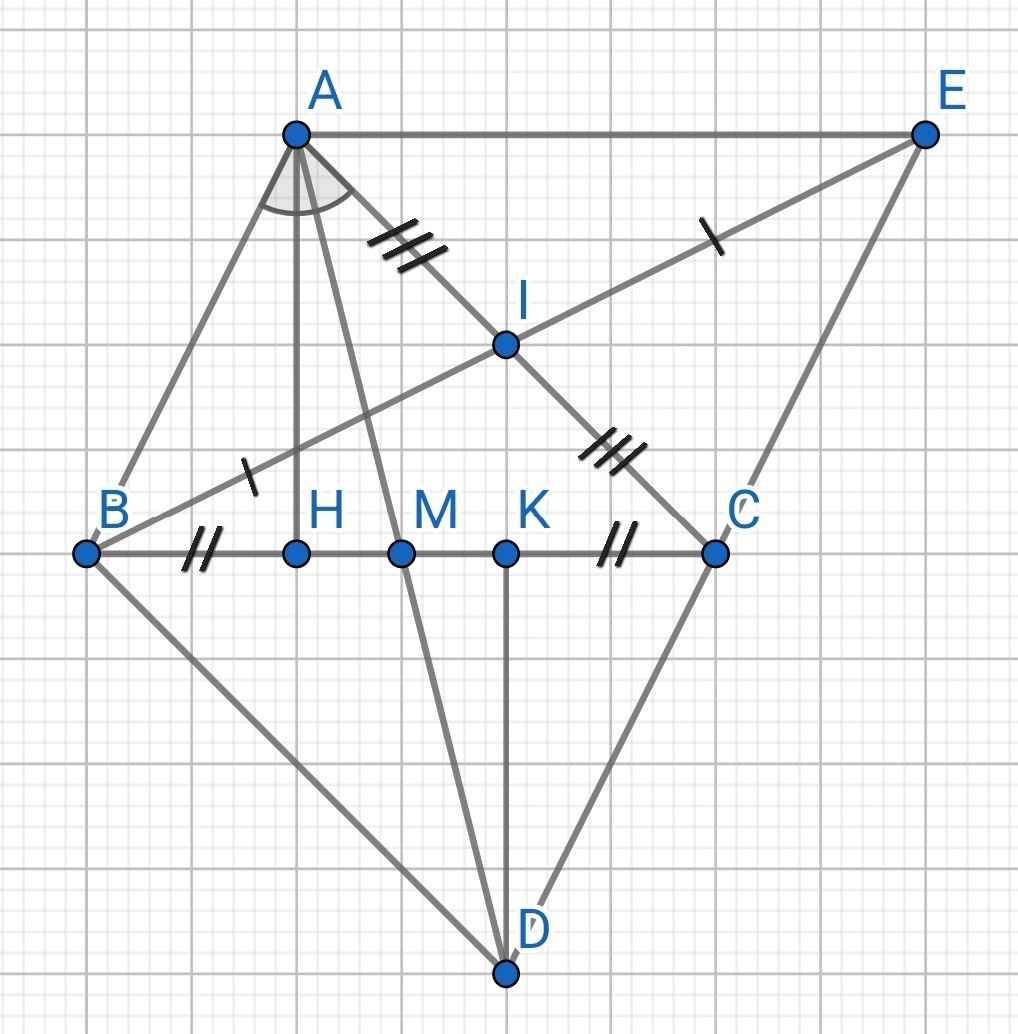 c) Do M là trung điểm của BC (gt)
c) Do M là trung điểm của BC (gt)
⇒ BM = MC
Xét hai tam giác vuông: ∆AHM và ∆DKM có:
MA = MD (gt)
∠AMH = ∠DMK (đối đỉnh)
⇒ ∆AHM = ∆DKM (cạnh huyền - góc nhọn)
⇒ HM = KM (hai cạnh tương ứng)
Ta có:
BK = BM + KM
CH = CM + HM
Mà BM = CM (cmt)
KM = HM (cmt)
⇒ BK = CH
d) Tứ giác ABDC có:
M là trung điểm của BC (gt)
M là trung điểm của AD (gt)
⇒ ABDC là hình bình hành
⇒ AB // DC và AB = DC
Tứ giác ABCE có:
I là trung điểm của AC (gt)
I là trung điểm của BE (gt)
⇒ ABCE là hình bình hành
⇒ AB // CE và AB = CE
Do AB // CE (cmt)
AB // DC (cmt)
⇒ C, D, E thẳng hàng (theo tiên đề Ơ-clít)
Ta có:
AB = CE (cmt)
AB = DC (cmt)
⇒ CD = CE
⇒ C là trung điểm của DE

Xét ΔMAH và ΔMCE có
MA=MC
\(\widehat{AMH}=\widehat{CME}\)(hai góc đối đỉnh)
MH=ME
Do đó: ΔMAH=ΔMCE
=>AH=CE

a: Xét ΔABD và ΔMCD có
DA=DM
\(\widehat{ADB}=\widehat{MDC}\)
DB=DC
Do đó: ΔABD=ΔMCD
b: Xét ΔAHD vuông tại H và ΔMKD vuông tại K có
DA=DM
\(\widehat{ADH}=\widehat{MDK}\)
Do đó: ΔAHD=ΔMKD
Suy ra: AH=MK