cho hai dây dẫn đồng chất, tiết diện đều, dây thứ nhất có chiều dài gấp đôi dây thứ hai. muốn điện trở dây thứ nhất gấp 3 lần điện trở dây thứ hai thì tiết diện của hai dây phải liên hệ với nhau như thế nào?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
29 tháng 11 2019
Đáp án A
Điện trở tỉ lệ nghịch với tiết diện:
R 1 / R 2 = S 2 / S 1 = 1 / 3 = > R 1 = R 2 . 1 / 3 = 6 / 3 = 2 Ω
14 tháng 11 2021
Dây thứ nhất có điện trở \(R_1=5\Omega\)
Theo bài: \(l_2=2l_1\)
Ta có: \(\dfrac{R_1}{R_2}=\dfrac{l_1}{l_2}\Rightarrow R_2=\dfrac{R_1\cdot l_2}{l_1}=5\cdot\dfrac{2l_1}{l_1}=5\cdot2=10\Omega\)
TK
20 tháng 12 2021
\(\dfrac{R_1}{R_2}=\dfrac{S_2}{S_1}=\dfrac{\dfrac{d_2^2}{4}\pi}{\dfrac{d_1^2}{4}\pi}=\dfrac{d_2^2}{d_1^2}=\dfrac{2}{8}\Rightarrow2d_1^2=8d_2^2\Leftrightarrow d_1=2d_2\)
Chọn D
16 tháng 10 2021
Điện trở dây thứ nhất: \(R_1=\rho\cdot\dfrac{l_1}{S_1}=8\Omega\)
Điện trở dây thứ 2: \(R_2=\rho\cdot\dfrac{l_2}{S_2}=\rho\cdot\dfrac{l_1}{2}:2S_1=\rho\cdot\dfrac{l_1}{4S_1}=\dfrac{1}{4}R_1\)
\(\Rightarrow R_2=\dfrac{1}{4}\cdot8=2\Omega\)
MH
17 tháng 10 2021
Điện trở dây thứ nhất: \(R_1=p.\dfrac{l1}{S1}=8\)Ω
Điện trở dây thứ2: \(R_2=p.\dfrac{l2}{S2}=p.\dfrac{l1}{2}:2S1=p.\dfrac{l1}{4S1}=\dfrac{1}{4}R_1\)
⇒R2=\(\dfrac{1}{4}\)⋅8=2Ω
17 tháng 10 2021
Ta có 2 dây dẫn được làm từ cùng một chất
\(\Rightarrow\dfrac{R_1}{R_2}=\dfrac{\dfrac{l_1}{S_1}}{\dfrac{l_2}{S_2}}\)\(\Rightarrow\dfrac{8}{R_2}=\dfrac{\dfrac{2l_2}{S_1}}{\dfrac{l_2}{2S_1}}=\dfrac{2l_2}{S_1}.\dfrac{2S_1}{l_2}=4\)
\(\Rightarrow R_2=\dfrac{8}{4}=2\left(\Omega\right)\)
21 tháng 11 2021
Câu 42.
Ta có:
\(\dfrac{R_1}{R_2}=\dfrac{\rho_1}{\rho_2}=2\)\(\Rightarrow\rho_2=\dfrac{\rho_1}{2}=\dfrac{2,8\cdot10^{-8}}{2}=1,4\cdot10^{-8}\left(\Omega.m\right)\)
Câu 43.
\(R_{tđ}=R_1+R_2=30+10=40\Omega\)
\(U_{max}\Leftrightarrow I_{min}\Rightarrow I=1A\)
\(\Rightarrow U_{max}=1\cdot40=40V\)
N
11 tháng 10 2021
Bạn tự làm tóm tắt nhé!
Bài 1:
Tiết diện của dây thứ nhất: \(R=p\dfrac{l}{S}\Rightarrow S=\dfrac{p.l}{R}=\dfrac{1,7.10^{-8}.10}{6}\simeq2,9.10^{-8}\)
Điện trở của dây thứ hai: \(R=p\dfrac{l}{S}=1,7.10^{-8}\dfrac{25}{2,9.10^{-8}}\simeq14,7\Omega\)
Bài 2:
Vì tiết diện dây thứ nhất là S1 = 2mm2 bằng \(\dfrac{1}{3}\) lần tiết diện dây thứ hai S2 = 6mm2
→ Điện trở của dây thứ hai nhỏ hơn ba lần điện trở của dây thứ nhất.
Bài 3:
Do điện trở tỉ lệ nghịch với tiết diện của dây dây, ta có:
\(\dfrac{S1}{S2}=\dfrac{R2}{R1}\Rightarrow R_2=R_1\dfrac{S_1}{S_2}=330\dfrac{2,5.10^{-6}}{12,5.10^{-6}}=66\Omega\)
N
5 tháng 11 2021
Ta có: \(\left\{{}\begin{matrix}R_1=\rho_1\dfrac{l_1}{S_1}\\R_2=\rho_2\dfrac{l_2}{S_2}\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}l_1=l_2\\S_1=S_2\\R_1=2R_2\end{matrix}\right.\)
\(\Rightarrow\dfrac{2R_2}{R_2}=\dfrac{\rho_1}{\rho_2}\)
\(\Rightarrow\rho_2=\dfrac{\rho_1}{2}=\dfrac{0,6.10^{-8}}{2}=3.10^{-9}=0,3.10^{-8}\left(\Omega m\right)\)
=> Chọn C
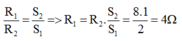
\(l_1=2l_2\\ R_1=3R_2\\ \rho_1=\rho_2\\ \Leftrightarrow\dfrac{R_1S_1}{l_1}=\dfrac{R_2S_2}{l_2}\\ \Leftrightarrow\dfrac{3R_2S_1}{2l_2}=\dfrac{R_2S_2}{l_2}\\ \Leftrightarrow3R_2S_1l_2=2l_2R_2S_2\\ \Leftrightarrow3S_1=2S_2\\ \Leftrightarrow S_1=\dfrac{2}{3}S_2\)