cho hình vuông có độ dài là đường chéo là 1.Trên mỗi cạnh của hình vuông các điểm M,N,P,Q. (M THUỘC AB,N THUỘC BC,P THUỘC PO) không nhỏ hơn 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


b: Xét ΔABD có
M là trung điểm của AB
Q là trung điểm của AD
Do đó: MQ là đường trung bình của ΔBAD
Suy ra: MQ//BD và \(MQ=\dfrac{BD}{2}\left(1\right)\)
Xét ΔBCD có
N là trung điểm của BC
P là trung điểm của CD
Do đó: NP là đường trung bình của ΔBCD
Suy ra: NP//BD và \(NP=\dfrac{BD}{2}\left(2\right)\)
Từ (1) và (2) suy ra NP//MQ và NP=MQ
Xét ΔADC có
Q là trung điểm của AD
P là trung điểm của CD
Do đó: QP là đường trung bình của ΔADC
Suy ra: QP//AC
mà AC\(\perp\)BD
nên QP\(\perp\)BD
mà MQ//BD
nên MQ\(\perp\)QP
hay \(\widehat{MQP}=90^0\)
Xét tứ giác MQPN có
MQ//NP
MQ=NP
Do đó: MQPN là hình bình hành
mà \(\widehat{MQP}=90^0\)
nên MQPN là hình chữ nhật
Xét tứ giác MQPN có
\(\widehat{MQP}+\widehat{MNP}=180^0\)
Do đó: MQPN là tứ giác nội tiếp
hay M,Q,P,N cùng thuộc 1 đường tròn

a) Xét tứ giác BIEM có
\(\widehat{IBM}\) và \(\widehat{IEM}\) là hai góc đối
\(\widehat{IBM}+\widehat{IEM}=180^0\)(\(90^0+90^0=180^0\))
Do đó: BIEM là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
⇔B,I,E,M cùng thuộc 1 đường tròn(đpcm)
b) Ta có: ABCD là hình vuông(gt)
nên BD là tia phân giác của \(\widehat{ABC}\)(Định lí hình vuông)
⇔BE là tia phân giác của \(\widehat{ABC}\)
⇔\(\widehat{ABD}=\dfrac{\widehat{ABC}}{2}=\dfrac{90^0}{2}=45^0\)
hay \(\widehat{IBE}=45^0\)
Ta có: BIEM là tứ giác nội tiếp(cmt)
nên \(\widehat{IBE}=\widehat{IME}\)(Định lí)
mà \(\widehat{IBE}=45^0\)(cmt)
nên \(\widehat{IME}=45^0\)
Vậy: \(\widehat{IME}=45^0\)

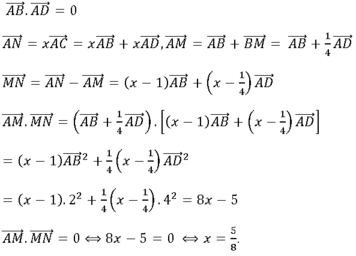
Chọn A.
Chú ý: Nếu có đúng bốn phương án như trong đề thi thì có thể dự đoán ngay phương án A sau khi vẽ hình