Bài khó quá nên nhờ ai học giỏi làm giúp em ạ! Em đang cần gấp :(
K
Khách
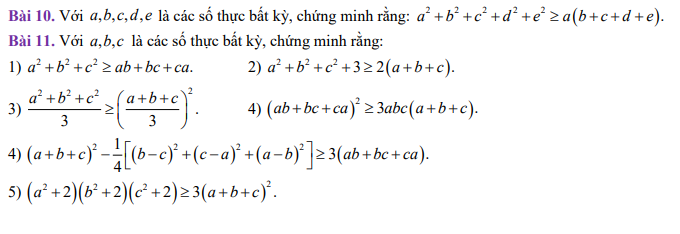
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 10 2023
Trước mắt tôi là một cánh đồng lúa rộng lớn, mênh mông đến tận chân trời. Những cây lúa cùng nhau hình thành một tấm thảm màu vàng óng ánh, như một biểu tượng của sự thịnh vượng và hy vọng. Những cánh cỏ màu xanh lợt nhấp nhô theo những luồng gió mượt mà, tạo nên một khung cảnh thôn quê dịu dàng và thanh bình. Những bông hoa lúa trắng xinh tinh khôi nở rộ trên các cánh đồng, tạo nên một cảm giác như là một màn trời mây trắng đẹp mắt. Những động tác của những người nông dân làm việc cật lực để trồng và chăm sóc cây lúa trở thành một hình ảnh sống động trong lòng cánh đồng. Ánh nắng mặt trời chiếu rọi từ trên cao, làm bừng sáng màu vàng của lúa chín, tạo nên một cảm giác ấm áp và tươi mát. Ông mặt trời rực rỡ và mềm mại, gửi tới cánh đồng lúa một món quà tuyệt vời - năng lượng mặt trời. Trên cánh đồng, tiếng cười vui tươi và cuộc sống rộn rã tựa như nhịp điệu của cuộc sống nông thôn. Đây không chỉ là một cánh đồng lúa, mà là một thế giới của sự sống, sự hy vọng và niềm tin. Cánh đồng lúa chín là một hình ảnh tuyệt đẹp, thể hiện sức sống và sự phát triển của nông nghiệp - nguồn sống chính của nhiều người trên toàn cầu.
EN
0
giúp em 3 bài này với ạ em đang cần gấp chiều em hc ròi ạ ai làm đc bài nào thì gửi luôn giúp em ạ
6 tháng 10 2021
lần sau đăng đúng lớp nhé đừng có mà lí do lí trấu
\(HPT\Leftrightarrow\left\{{}\begin{matrix}x+y=1\\2y=-2a\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-a=1\\y=-a\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1+a\\y=-a\end{matrix}\right.\\ x>y\Leftrightarrow1+a>-a\Leftrightarrow2a>-1\Leftrightarrow a>-\dfrac{1}{2}\)
6 tháng 10 2021
nhìn cái đề bài nó cứ sai sai
ê mà sao lớp 1 mà cô giáo cho đề bài này được
4 tháng 12 2021
a) Xét tam giác ABE và tam giác ACE có:
+ AE chung.
+ AB = AC (gt).
+ BE = CE (E là trung điểm của BC).
=> Tam giác ABE = Tam giác ACE (c - c - c).
b) Xét tam giác ABC có: AB = AC (gt).
=> Tam giác ABC cân tại A.
Mà AE là đường trung tuyến (E là trung điểm của BC).
=> AE là phân giác ^BAC (Tính chất các đường trong tam giác cân).
c) Xét tam giác ABC cân tại A có:
AE là phân giác ^BAC (cmt).
=> AE là đường cao (Tính chất các đường trong tam giác cân).
=> AE \(\perp\) BC.
Xét tam giác BIE và tam giác CIE:
+ IE chung.
+ BE = CE (E là trung điểm của BC).
+ ^BEI = ^CEI ( = 90o).
=> Tam giác BIE = Tam giác CIE (c - g - c).
14 tháng 4 2022
Bài 3:
Số học sinh kém là:
40-8-10-20=2(bạn)
Tỉ số phần trăm giữa số học sinh giỏi so với lớp là:
8:40=20%
Tỉ số phần trăm giữa số học sinh khá so với lớp là:
20:40=50%
Tỉ số phần trăm giữa số học sinh trung bình so với lớp là:
10:40=25%
Tỉ số phần trăm giữa số học sinh yếu so với lớp là:
2:40=5%
7 tháng 6 2023
Trong kì I, số học sinh giỏi của lớp 6A = \(\dfrac{2}{7}\) số học sinh còn lại
=> Số học sinh giỏi chiếm \(\dfrac{2}{9}\) số học sinh cả lớp
Cuối năm số học sinh giỏi của lớp 6A = \(\dfrac{1}{2}\) số học sinh còn lại
=> Số học sinh giỏi của lớp 6A chiếm \(\dfrac{1}{3}\) số học sinh cả lớp
5 học sinh ứng với phân số:
\(\dfrac{1}{3}\) - \(\dfrac{2}{9}\) = \(\dfrac{1}{9}\) ( tổng số học sinh lớp 6A)
Số học sinh lớp 6A là:
5 : \(\dfrac{1}{9}\) = 45 ( học sinh)
Đáp số : 45 học sinh
1N
2
23 tháng 5 2022
Điện trở đèn:
\(R=\dfrac{U^2}{P}=\dfrac{12^2}{6}=24\Omega\)
Hai điện trở \(R_2;R_3\) mắc song song nhau\(\Rightarrow R_{23}=\dfrac{R_2\cdot R_3}{R_2+R_3}=\dfrac{20\cdot20}{20+20}=10\Omega\)
Điện trở tương đương:
\(R=R_Đ+R_{23}=24+10=34\Omega\)
Dòng điện qua mạch lúc này: \(I=\dfrac{U}{R}=\dfrac{15}{34}=0,44A\)
23 tháng 5 2022
b, Điển trở R1 của bóng đèn:
Từ công thức: \(P=\dfrac{U^2}{R}\Rightarrow R_1+\dfrac{U^2}{P}=12^2:6=24\Omega\)
Điện trở tương đương của đoạn mạch:
Vì R1 nt \(\left(R_2//R_3\right)\) nên \(R_{tđ}=R_1+\dfrac{R_2.R_3}{R_2+R_3}=24+\dfrac{20.20}{20+20}=34\Omega\)
Số chỉ của ampe kế: \(I=\dfrac{U}{R}=15:34=0,44A\)
\(10,\\ a^2+b^2+c^2+d^2+e^2\ge a\left(b+c+d+e\right)\\ \Leftrightarrow4a^2+4b^2+4c^2+4d^2+4e^2\ge4ab+4ac+4ad+4ae\\ \Leftrightarrow\left(a^2-4ab+4b^2\right)+\left(a^2-4ac+4c^2\right)+\left(a^2-4ad+4d^2\right)+\left(a^2-4ae+4e^2\right)\ge0\\ \Leftrightarrow\left(a-2b\right)^2+\left(a-2c\right)^2+\left(a-2d\right)^2+\left(a-2e\right)^2\ge0\left(luôn.đúng\right)\)
Dấu \("="\Leftrightarrow\dfrac{a}{2}=b=c=d=e\)
\(4,\Leftrightarrow a^2+b^2+c^2+2ab+2bc+2ac-\dfrac{1}{4}\left(2a^2+2b^2+2c^2-2ab-2ac-2bc\right)\ge3ab+3bc+3ca\\ \Leftrightarrow a^2+b^2+c^2+2ab+2bc+2ac-\dfrac{1}{2}a^2-\dfrac{1}{2}b^2-\dfrac{1}{2}c^2-ab-bc-ac\ge0\\ \Leftrightarrow\dfrac{1}{2}a^2+\dfrac{1}{2}b^2+\dfrac{1}{2}c^2+ab+ac+bc\ge0\\ \Leftrightarrow a^2+b^2+c^2+2ab+2bc+2ac\ge0\\ \Leftrightarrow\left(a+b+c\right)^2\ge0\left(luôn.đúng\right)\)
Dấu \("="\Leftrightarrow a+b+c=0\)