Cho các số dương a,b,c,d biết \(\dfrac{a}{1+a}+\dfrac{b}{1+b}+\dfrac{c}{1+c}+\dfrac{d}{1+d}\le1.CMRabcd\le\dfrac{1}{81}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Áp dụng BĐT AM-GM ta có:
\(\dfrac{1}{a+1}\ge1-\dfrac{1}{b+1}+1-\dfrac{1}{c+1}+1-\dfrac{1}{d+1}\)
\(=\dfrac{b}{b+1}+\dfrac{c}{c+1}+\dfrac{d}{d+1}\)\(\ge3\sqrt[3]{\dfrac{bcd}{\left(b+1\right)\left(c+1\right)\left(d+1\right)}}\)
Tương tự cho 3 BĐT còn lại cũng có:
\(\dfrac{1}{1+b}\ge3\sqrt[3]{\dfrac{acd}{\left(a+1\right)\left(c+1\right)\left(d+1\right)}};\dfrac{1}{c+1}\ge3\sqrt[3]{\dfrac{abd}{\left(a+1\right)\left(b+1\right)\left(d+1\right)}};\dfrac{1}{d+1}\ge3\sqrt[3]{\dfrac{abc}{\left(a+1\right)\left(b+1\right)\left(c+1\right)}}\)
Nhân theo vế 4 BĐT trên ta có:
\(\dfrac{1}{\left(a+1\right)\left(b+1\right)\left(c+1\right)\left(d+1\right)}\ge81\sqrt[3]{\left(\dfrac{abcd}{\left(a+1\right)\left(b+1\right)\left(c+1\right)\left(d+1\right)}\right)^3}\)
\(\Leftrightarrow1\ge81abcd\Leftrightarrow abcd\le\dfrac{1}{81}\)

Từ giả thiết, ta có:
\(\dfrac{1}{1+a}\ge1-\dfrac{1}{1+b}+1-\dfrac{1}{1+c}+1-\dfrac{1}{1+d}=\dfrac{b}{1+b}+\dfrac{c}{c+1}+\dfrac{d}{d+1}\ge3\sqrt[3]{\dfrac{b.c.d}{\left(1+b\right)\left(1+c\right)\left(1+d\right)}}\)
Tương tự:
\(\dfrac{1}{1+b}\ge3\sqrt[3]{\dfrac{cda}{\left(1+a\right)\left(1+c\right)\left(1+d\right)}}\)
\(\dfrac{1}{1+c}\ge3\sqrt[3]{\dfrac{abd}{\left(1+a\right)\left(1+b\right)\left(1+d\right)}}\)
\(\dfrac{1}{1+d}\ge3\sqrt[3]{\dfrac{abc}{\left(1+a\right)\left(1+b\right)\left(1+c\right)}}\)
Nhân vế theo vế 4 BĐT vừa chứng minh rồi rút gọn ta được:
\(abcd\le\dfrac{1}{81}\left(đpcm\right)\)
cho ba số dương \(0\le a\le b\le c\le1\) CMR \(\dfrac{a}{bc+1}+\dfrac{b}{ac+1}+\dfrac{c}{ab+1}\le2\)

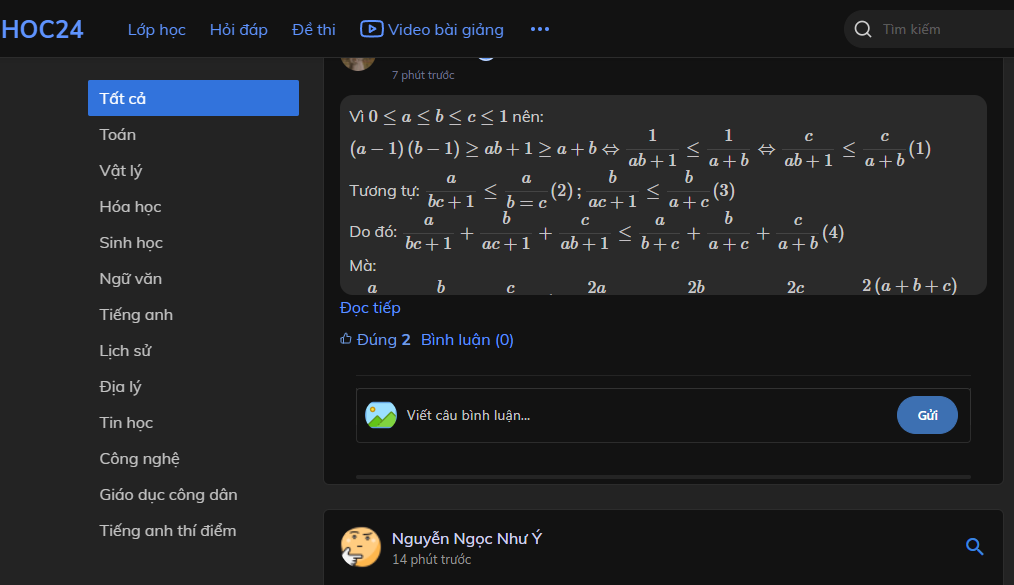
Vì \(0\le a\le b\le c\le1\) nên:
\(\left(a-1\right)\left(b-1\right)\ge ab+1\ge a+b\Leftrightarrow\dfrac{1}{ab+1}\le\dfrac{1}{a+b}\Leftrightarrow\dfrac{c}{ab+1}\le\dfrac{c}{a+b}\left(1\right)\)
Tương tự: \(\dfrac{a}{bc+1}\le\dfrac{a}{b=c}\left(2\right);\dfrac{b}{ac+1}\le\dfrac{b}{a+c}\left(3\right)\)
Do đó: \(\dfrac{a}{bc+1}+\dfrac{b}{ac+1}+\dfrac{c}{ab+1}\le\dfrac{a}{b+c}+\dfrac{b}{a+c}+\dfrac{c}{a+b}\left(4\right)\)
Mà: \(\dfrac{a}{b+c}+\dfrac{b}{a+c}+\dfrac{c}{a+b}\le\dfrac{2a}{a+b+c}+\dfrac{2b}{a+b+c}+\dfrac{2c}{a+b+c}=\dfrac{2\left(a+b+c\right)}{a+b+c}=2\left(5\right)\)
Từ (4) và (5) suy ra \(\dfrac{a}{bc+1}+\dfrac{b}{ac+1}+\dfrac{c}{ab+1}\left(đpcm\right)\)

Bunhiacopxki:
\(\left(a^2+b+c+d\right)\left(1+b+c+d\right)\ge\left(a+b+c+d\right)^2=16\)
\(\Rightarrow\dfrac{1}{a^2+b+c+d}\le\dfrac{1+b+c+d}{16}\)
Tương tự:
\(\dfrac{1}{b^2+c+d+a}\le\dfrac{1+c+d+a}{16}\) ; \(\dfrac{1}{c^2+d+a+b}\le\dfrac{1+d+a+b}{16}\)
\(\dfrac{1}{d^2+a+b+c}\le\dfrac{1+a+b+c}{16}\)
Cộng vế:
\(P\le\dfrac{4+3\left(a+b+c+d\right)}{16}=1\) (đpcm)
Dấu "=" xảy ra khi \(a=b=c=d=1\)


\(\dfrac{b}{1+b}+\dfrac{c}{1+c}+\dfrac{d}{1+d}\le1-\dfrac{a}{1+a}=\dfrac{1}{1+a}\)
\(\Rightarrow\dfrac{1}{1+a}\ge\dfrac{b}{1+b}+\dfrac{c}{1+c}+\dfrac{d}{1+d}\ge3\dfrac{\sqrt[3]{bcd}}{\sqrt[3]{\left(1+b\right)\left(1+c\right)\left(1+d\right)}}\)
Chứng minh tương tự ta có:
\(\dfrac{1}{1+b}\ge3\dfrac{\sqrt[3]{acd}}{\sqrt[3]{\left(1+a\right)\left(1+c\right)\left(1+d\right)}}\)
\(\dfrac{1}{1+c}\ge3\dfrac{\sqrt[3]{abd}}{\sqrt[3]{\left(1+a\right)\left(1+b\right)\left(1+d\right)}}\)
\(\dfrac{1}{1+d}\ge3\dfrac{\sqrt[3]{abc}}{\sqrt[3]{\left(1+a\right)\left(1+b\right)\left(1+c\right)}}\)
Nhân vế với vế của các BĐT trên ta được:
\(\dfrac{1}{\left(1+a\right)\left(1+b\right)\left(1+c\right)\left(1+d\right)}\ge81\dfrac{abcd}{\left(1+a\right)\left(1+b\right)\left(1+c\right)\left(1+d\right)}\)
\(\Rightarrow81abcd\le1\Rightarrow abcd\le\dfrac{1}{81}\)
Dấu "=" xảy ra khi \(a=b=c=d=\dfrac{1}{3}\)