cho tứ giác ABCD .Gọi E:F;G;H lần lươt là trung điểm của AB,AC,CD,DB
a) Chứng minh rằng EFGH là hình bình hành
b)các cạnh ad và BC của tứ giác ABCD cần có điều kiện gì để tứ giác EFGH là :hình chữ nhật,hình thoi,hình vuông,
giải giúp mình với ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Hạ CH vuông góc với OB tại H. Theo quan hệ đường xiên hình chiếu:
\(CH\le OC\Leftrightarrow CH.OB\le OC.OB\Leftrightarrow2.S_{BOC}\le OC.OB\)(Do \(S_{BOC}=\frac{CH.OB}{2}\))
Áp dụng BĐT Cauchy, ta có: \(OC.OB\le\frac{OC^2+OB^2}{2}\)
\(\Rightarrow2.S_{BOC}\le\frac{OC^2+OB^2}{2}\left(1\right)\). Chứng minh tương tự ta được:
\(2.S_{AOB}\le\frac{OA^2+OB^2}{2}\left(2\right);2.S_{DOC}\le\frac{OD^2+OC^2}{2}\left(3\right);2.S_{AOD}\le\frac{OA^2+OD^2}{2}\left(4\right)\)
Cộng (1); (2); (3) và (4) theo vế:
\(2.\left(S_{BOC}+S_{AOB}+S_{DOC}+S_{AOD}\right)\le\frac{2.\left(OA^2+OB^2+OC^2+OD^2\right)}{2}\)
\(\Rightarrow2S\le OA^2+OB^2+OC^2+OD^2\)=> ĐPCM.
\(2.S_{BOC}\le OC.OB\). Dấu "=" xảy ra <=> OC vuông góc với OB
\(OC.OB\le\frac{OC^2+OB^2}{2}\). Dấu "=" xảy ra <=> OC=OB
Suy ra \(2.S_{BOC}\le\frac{OC^2+OB^2}{2}\). Dấu "=" xảy ra <=> \(\Delta\)BOC vuông cân tại O
Tương tự với các tam giác AOB; AOD; DOC.
Vậy dấu "=" xảy ra <=> Tứ giác ABCD là hình vuông và O là tâm của hình vuông này.

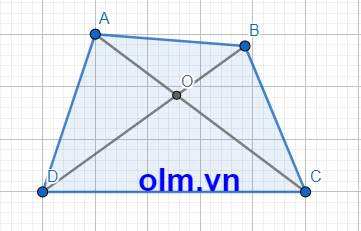
a, Xét \(\Delta\) AOB có: AO+OB > AB (trong tam giác tổng hai cạnh luôn lớn hơn cạnh còn lại)
Tương tự ta có: OC + OD > DC
OA + OD > AD
OB + OC > BC
Cộng vế với vế ta có:
OA+OB+OC+OD+OA+OD+OB+OC > AB +DC+AD+BC
(OA+OC)\(\times\)2 + (OB + OD)\(\times\)2 > PABCD
AC \(\times\) 2 + BD \(\times\) 2 > PABCD
AC + BD > \(\dfrac{P_{ABCD}}{2}\) (đpcm)
b, Xét \(\Delta\) ABD có: AB + AD > BD (trong tam giác tổng hai cạnh bao giờ cũng lớn hơn cạnh còn lại)
Tương tự ta có: AD + DC > AC
DC + CB > DB
CB + AB > AC
Cộng vế với vế ta có:
AB+AD+AD+DC+DC+CB+CB+AB >BD+ AC+DB+AC
2AB+2BC+2CD+2AD> 2AC + 2BD
2(AB + BC + CD + AD) > 2(AC + BD)
AB + BC + CD + AD > AC + BD
PABCD > AC + BD (đpcm)

a: Xét ΔABD có
M là trung điểm của AB
Q là trung điểm của AD
Do đó: MQ là đường trung bình của ΔABD
Suy ra: MQ//BD và \(MQ=\dfrac{BD}{2}\)(1)
Xét ΔBCD có
N là trung điểm của BC
P là trung điểm của CD
Do đó: NP là đường trung bình của ΔBCD
Suy ra: NP//BD và \(NP=\dfrac{BD}{2}\left(2\right)\)
Từ (1) và (2) suy ra MQ//NP và MQ=NP
hay MQPN là hình bình hành

Chứng minh EFGH là hình bình hành. Để EFGH là hình chữ nhật thì
Þ H E F ^ = 90 0 ⇒ H E ⊥ E F
Þ AC ^BD.
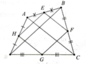

a) Xét ΔABC có
M là trung điểm của AB(gt)
N là trung điểm của BC(gt)
Do đó: MN là đường trung bình của ΔABC(Định nghĩa đường trung bình của tam giác)
Suy ra: MN//AC và \(MN=\dfrac{AC}{2}\)(Định lí 2 về đường trung bình của tam giác)(1)
Xét ΔADC có
Q là trung điểm của AD(gt)
P là trung điểm của CD(gt)
Do đó: QP là đường trung bình của ΔADC(Định nghĩa đường trung bình của tam giác)
Suy ra: QP//AC và \(QP=\dfrac{AC}{2}\)(Định lí 2 về đường trung bình của tam giác)(2)
Từ (1) và (2) suy ra MN//PQ và MN=PQ
Xét tứ giác MNPQ có
MN//PQ(cmt)
MN=PQ(cmt)
Do đó: MNPQ là hình bình hành(Dấu hiệu nhận biết hình bình hành)
b)
Xét ΔABD có
M là trung điểm của AB(gt)
Q là trung điểm của AD(gt)
Do đó: MQ là đường trung bình của ΔADB(Định nghĩa đường trung bình của tam giác)
Suy ra: \(MQ=\dfrac{BD}{2}\)(Định lí 2 về đường trung bình của tam giác)
Hình bình hành MNPQ trở thành hình vuông khi \(\left\{{}\begin{matrix}\widehat{MQP}=90^0\\MQ=QP\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}AB\perp CD\\AB=CD\end{matrix}\right.\)
Hình bình hành MNPQ trở thành hình vuông khi

a: Xét ΔABD có
E là trung điểm của AB
H là trung điểm của AD
Do đó: EH là đường trung bình của ΔABD
Suy ra: EH//BD và \(EH=\dfrac{BD}{2}\left(1\right)\)
Xét ΔBCD có
F là trung điểm của BC
G là trung điểm của DC
Do đó: FG là đường trung bình của ΔBCD
Suy ra: FG//BD và \(FG=\dfrac{BD}{2}\left(2\right)\)
Từ (1) và (2) suy ra EH//GF và EH=GF
hay EHGF là hình bình hành