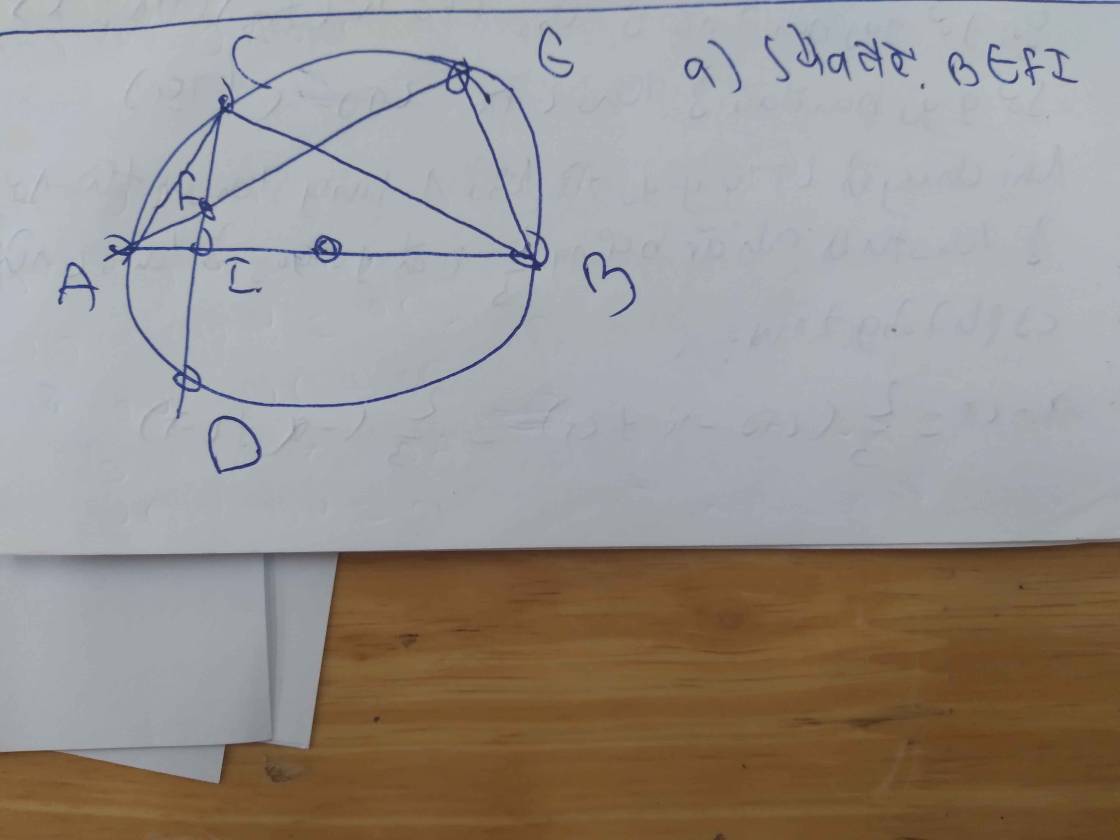
Cho (0) đường kính AB=2R. Một dây CD không đi qua tâm 0, sao cho góc COD bằng 90* và CD cắt đường thẳng AB tại E ( D nằm giữa 2 điểm E và C) . Biết OE=2R. Tính độ dài EC và ED theo R
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TT
19 tháng 10 2018
Sửa lại đề của bạn là:
Cho đường tròn tâm O đường kính AB=2R. Dây cung CD không đi qua tâm O sao cho góc COD=90 độ. CD cắt AB ở E (D nằm giữa E và C ) sao cho OE=2R . Tính EC và ED theo R.
Bài làm:
Kẻ \(OM\perp CE\)và \(BN\perp CE\). Khi đó
Do COD là tam giác vuông cân nên \(CD=R\sqrt{2}\)và \(OM=MD=\frac{R\sqrt{2}}{2}\)
Ta có EB = BO và BN // OM nên EN = MN
suy ra NB là đường trung bình của tam giác vuông EMO nên \(NB=\frac{OM}{2}=\frac{R\sqrt{2}}{4}\)
Xét tam giác vuông ENB có \(EN=\sqrt{EB^2-BN^2}=\sqrt{R^2-\frac{2R^2}{4^2}}=\frac{R\sqrt{14}}{4}\)
mà MN = EN suy ra
\(DN=MN-MD=\frac{R\sqrt{14}}{4}-\frac{R\sqrt{2}}{2}=\frac{R\sqrt{14}-2R\sqrt{2}}{4}\)
Vậy \(ED=EN+ND=\frac{R\sqrt{14}}{4}+\frac{R\sqrt{14}-2R\sqrt{2}}{4}=\frac{R\sqrt{14}-R\sqrt{2}}{2}\)
\(EC=ED+DC=\frac{R\sqrt{14}-R\sqrt{2}}{2}+R\sqrt{2}=\frac{R\sqrt{14}+R\sqrt{2}}{2}\)
TD
29 tháng 8 2016
Theo đầu bài thì CD cắt AB ở E (D nằm giữa E và C) nhưng D không thể nằm giữa E và C. DE = 2R = AB nhưng DE chỉ bằng R nên DE không thể bằng AB nên bài toán này không có cách giải.
10 tháng 12 2023
a: kẻ OH\(\perp\)CD tại H
Ta có: OH\(\perp\)CD
AP\(\perp\)CD
QB\(\perp\)CD
Do đó: OH//AP//QB
Xét hình thang ABQP(AP//QB) có
O là trung điểm của AB
OH//AP//BQ
Do đó: H là trung điểm của PQ
=>HP=HQ
Ta có: ΔOCD cân tại O
mà OH là đường cao
nên H là trung điểm của CD
=>HC=HD
Ta có: HC+CP=HP
HD+DQ=HQ
mà HP=HQ và HC=HD
nên CP=DQ
b: Ta có: ΔOCD vuông tại O
=>\(OC^2+OD^2=CD^2\)
=>\(CD^2=R^2+R^2=2R^2\)
=>\(CD=R\sqrt{2}\)
Xét ΔOAC có OA=OC=AC=R
nên ΔOAC đều
=>\(\widehat{CAO}=60^0\)
=>\(\widehat{CAB}=60^0\)
Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
Xét ΔCAB vuông tại C có \(sinCAB=\dfrac{CB}{AB}\)
=>\(\dfrac{CB}{2R}=sin60=\dfrac{\sqrt{3}}{2}\)
=>\(CB=R\sqrt{3}\)