K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

AT
13 tháng 8 2016
Nhận thấy tứ giác MFNE có góc M và N vuông --> góc MFN+góc MEN= 2 vuông (*)
Lại có các tam giác AFB và MEN đồng dạng (vì có góc NME=gocFAB và góc MNE =góc FBA), suy ra góc AFB=góc MEN --> góc MFN=góc MEN (**), từ (*); (**) suy ra góc MFN=góc MEN =1 vuông
--> tứ giác MENF là hình chữ nhật, từ đó dễ dàng suy ra tiếp FE vuông góc với AB
b) Gọi I ; K lần lượt là trung điểm của O1O2 và MN. Áp dụng Talét dễ dàng tính được IK=5
--> KD^2=ID^2-IK^2 =9^2 -5^2 =56 --> CD=2.KD= 4√14

CM
4 tháng 3 2019
Giả sử vẽ được như hình bs.18
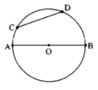
Dùng compa so sánh được CD < AB.
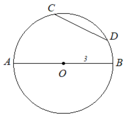
Theo đầu bài thì CD cắt AB ở E (D nằm giữa E và C) nhưng D không thể nằm giữa E và C. DE = 2R = AB nhưng DE chỉ bằng R nên DE không thể bằng AB nên bài toán này không có cách giải.