Tìm nghiệm nguyên của phương trình: 6x2+19y2+24x-2+12xy-725=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HH
2
V
22 tháng 10 2019
6x2+19y2+24x-2y+12xy-725=0
\(\Leftrightarrow6x^2+\left(12y+24\right)x-2y+19y^2-725=0\)
\(\Leftrightarrow\Delta=\left(12y+24\right)^2-4.6.\left(-2y+19y^2-725\right)\)
\(\Leftrightarrow144y^2+576y+576+48y-456y^2+17400\)
bữa sau sẽ trả lời tiếp
LH
18 tháng 3 2020
Với \(x,y\in Z\)
\(6x^2+19y^2+24x-2y+12xy-725=0\)
\(\Leftrightarrow6x^2+\left(12xy+24x\right)+19y^2-2y-725=0\)
\(\Leftrightarrow6x^2+\left(12y+24\right)x+19y^2-2y-725=0\)
\(\Leftrightarrow6x^2+2\left(6y+12\right)x+19y^2-2y-725=0\) \(\left(a=6,b'=6y+12,c=19y^2-2y-725\right)\)
\(\Delta'=\left(6y+12\right)^2-6\left(19y^2-2y-725\right)=36y^2+144y+144-114y^2+12y+4350\)
\(\Delta'=-78y^2+156y+4494=-78\left(y^2-2y+1\right)+78+4494=-78\left(y-1\right)^2+4572\)
PT có nghiệm \(\Leftrightarrow\Delta'\ge0\Leftrightarrow-78\left(y-1\right)^2+4572\ge0\Leftrightarrow-78\left(y-1\right)^2\ge-4572\)
\(\Leftrightarrow\left(y-1\right)^2\le\frac{762}{13}\)
\(\Leftrightarrow-\frac{\sqrt{9906}}{13}\le y-1\le\frac{\sqrt{9906}}{13}\), mà \(y\in Z\) \(\Rightarrow-7\le y-1\le7\left(1\right)\)
Với PT có nghiệm, ta có: \(x=\frac{-b'\pm\sqrt{\Delta'}}{a}\)
\(\hept{\begin{cases}x_1+x_2=\frac{-b}{a}=\frac{-\left(12y+24\right)}{6}=-2y-4\\x_1x_2=\frac{c}{a}=\frac{19y^2-2y-725}{6}=\frac{y^2-2y+1+18y^2-726}{6}=3y^2-121+\frac{\left(y-1\right)^2}{6}\end{cases}}\)
Để \(x\in Z\), thì \(\hept{\begin{cases}x_1+x_2\in Z\\x_1x_2\in Z\end{cases}}\Leftrightarrow\hept{\begin{cases}-2y-4\in Z\\3y^2-121+\frac{\left(y-1\right)^2}{6}\in Z\end{cases}\Leftrightarrow}\frac{\left(y-1\right)^2}{6}\in Z\) (vì \(y\in Z\))
Và \(\Delta'\) là số chính phương.
* \(\frac{\left(y-1\right)^2}{6}\in Z\Leftrightarrow\left(y-1\right)^2⋮6\Leftrightarrow y-1⋮6\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\) \(\Rightarrow y-1\in\left\{-6;0;6\right\}\Leftrightarrow y\in\left\{-5;1;7\right\}\)
* \(\Delta'\) là số chính phương \(\Leftrightarrow-78\left(y-1\right)^2+4572\) là số chính phương
- Thử \(y=-5\), thì \(\Delta'=-78\left(-5-1\right)^2+4572=-2808+4572=1764\) (1764 là số chính phương)
- Thử \(y=1\), thì \(\Delta'=-78\left(1-1\right)^2+4572=4572\) (4572 không phải là số chính phương)
- Thử \(y=7\), thì \(\Delta'=-78\left(7-1\right)^2+4572=-2808+4572=1764\) (1764 là số chính phương)
Từ đó, với \(y\in\left\{-5;7\right\}\) thì \(\Delta'=1764\) là số chính phương. \(\Rightarrow\sqrt{\Delta'}=42\)
PT có nghiệm thì:
\(x=\frac{-b'\pm\sqrt{\Delta'}}{a}=\frac{-6y-12\pm42}{6}=-y-2\pm7\)
- Với \(y=-5\), thì \(x=5-2\pm7\Leftrightarrow x\in\left\{-4;10\right\}\) (tmđk)
- Với \(y=7\), thì \(x=-7-2\pm7\Leftrightarrow x\in\left\{-16;-2\right\}\) (tmđk)
Vậy phương trình có các nghiệm nguyên \(\left(x;y\right)=\left(-4;-5\right),\left(10;-5\right),\left(-16;7\right),\left(-2;7\right)\).
FT
0
6 tháng 8 2021
6x2-3xy+17x-4y+5=0
⇔ -3xy-4y=-6x2-17x-5
⇔ 3xy+4y=6x2+17x+5
⇔ y(3x+4)=6x2+17x+5
6x2+17x+5 ⋮ 3x-4 vì x, y ∈ Z
⇔ 6x2+17x+12-7 ⋮ 3x+4
⇔ 6x2+8x+9x+12-7 ⋮ 3x+4
⇔ 2x(3x+4)+3(3x+4)-7 ⋮ 3x+4
=> 7 ⋮ 3x+4
=> 3x+4 ∈ Ư(7)={-1,1,-7,7}
3x+4=1 ⇔ x=-1 (lấy)
3x+4=-1 ⇔ x=\(\dfrac{-5}{3}\) (loại)
3x+4=-7 ⇔ x=\(\dfrac{-11}{3}\)(loại)
3x+4=7 ⇔ x=1 (lấy)
thay vào tính thì y={-6,4} (bạn tự làm nhá)
vậy (x,y)={(-1,1),(-6,4)}
CM
1 tháng 12 2019
Phương trình 16x2 − 24x + 9 = 0
có a = 16; b’ = −12; c = 9 suy ra
Δ ' = b ' 2 − a c = (−12)2 – 9.16 = 0
Nên phương trình có nghiệm kép
Đáp án cần chọn là: C
CM
4 tháng 11 2018
Đáp án C.
⇒ Chia 2 vế phương trình cho x 3 ta được:
x 3 + 1 x 3 + 3 x 2 + 1 x 2 + 6 x + 1 x = m (*)
Đặt t = x + 1 x ⇒ t ≥ 2 , phương trình (*) m = t 3 + 3 t 2 + t - 6
Xét f ( t ) = t 3 + 3 t 2 + 3 t - 6 trên ( - ∞ ; - 2 ] ∪ [ 2 ; + ∞ )
f ' ( t ) = 0 ⇔ t = - 1
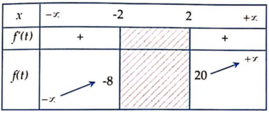
Bảng biến thiên:
⇒ f ( t ) ∈ ( - ∞ ; - 8 ] ∪ [ 20 ; + ∞ ) ∀ t ∈ ( - ∞ ; - 2 ] ∪ [ 2 ; + ∞ )
⇒ Phương trình f (t) vô nghiệm ⇔ m ∈ - 8 ; 20
⇒ Có 27 giá trị m nguyên thỏa mãn.
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 10 2019
a/ Hình như bạn ghi nhầm đề
b/ \(\Leftrightarrow x^2y^2-7y^2=x^2+2xy+y^2\)
\(\Leftrightarrow y^2\left(x^2-7\right)=\left(x+y\right)^2\)
- Với \(y=0\Rightarrow x=0\)
- Với \(y\ne0\) do \(y^2\) và \(\left(x+y\right)^2\) đều là số chính phương \(\Rightarrow x^2-7\) là SCP
Đặt \(x^2-7=k^2\Leftrightarrow\left(x-k\right)\left(x+k\right)=7\)
Phương trình ước số cơ bản
c/ \(\Leftrightarrow\left(x-y\right)^3+3xy\left(x-y\right)=xy+25\)
\(\Leftrightarrow\left(x-y\right)^3-25=xy\left(1-3\left(x-y\right)\right)\)
Đặt \(\left\{{}\begin{matrix}x-y=a\\xy=b\end{matrix}\right.\) \(\Rightarrow a^2\ge-4b\Rightarrow b\ge-\frac{a^2}{4}\)
\(\Rightarrow a^3-25=b\left(1-3a\right)\)
\(\Leftrightarrow b=\frac{a^3-25}{1-3a}\ge-\frac{a^2}{4}\)
Do \(a\) nguyên \(\Rightarrow1\le a\le4\)
\(\Rightarrow a=\left\{1;2;3;4\right\}\) thay vào chỉ có \(a=1\Rightarrow b=12\) thỏa mãn
\(\Rightarrow\left\{{}\begin{matrix}x-y=1\\xy=12\end{matrix}\right.\) \(\Rightarrow\left(x;y\right)=\left(4;3\right);\left(-3;-4\right)\)
17 tháng 10 2021
\(\Leftrightarrow x^4-x^3+x^3-x^2-8x^2+8x+16x-16=0\\ \Leftrightarrow\left(x-1\right)\left(x^3+x^2-8x+16\right)=0\\ \Leftrightarrow\left(x-1\right)\left(x^3+4x^2-3x^2-12x+4x+16\right)=0\\ \Leftrightarrow\left(x-1\right)\left(x+4\right)\left(x^2-3x+4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\x=-4\\\left(x-\dfrac{3}{2}\right)^2+\dfrac{7}{4}=0\left(vô.n_o\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-4\end{matrix}\right.\)