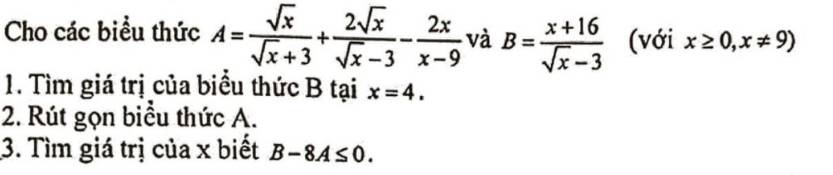Làm cho em câu 4c với câu 5 vs ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
BT
0
1 tháng 1 2022
Tham khảo:
Quê hương với mỗi người là một miền kí ức thiêng liêng. Đó có thể là một vùng quê thanh bình, thơ mộng cũng có thể là một thành phố năng động, sôi động. Với tôi, quê hương là một vùng trung du yên ả với đồi núi nhấp nhô, trập trùng. Mảnh đất ấy có con sông nhỏ đưa nước về tưới mát những ruộng lúa, nương dâu xanh tốt. Đất vùng trung du không được màu mỡ, tươi tốt như phù sa đồng bằng, đất chỉ thích hợp với trồng hoa màu và những rừng cọ, đồi chè. Quê hương tôi bình yên đến lạ, là những câu hát vang xa trên những khoảng đồi của người làm nương rẫy, là chia nhau củ sắn ngọt bùi của những người hàng xóm thân quen. Những kỉ niệm ngọt ngào về quê hương sẽ là hàng trang theo tôi suốt cuộc đời.
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 6 2021
4a.
\(y'=\dfrac{1}{cos^2x}+cosx-2=\dfrac{cos^3x-2cos^2x+1}{cos^2x}=\dfrac{\left(1-cosx\right)\left(1+cosx\left(1-cosx\right)\right)}{cos^2x}>0\) ; \(\forall x\in\left(0;\dfrac{\pi}{2}\right)\)
\(\Rightarrow\) Hàm đồng biến trên \(\left(0;\dfrac{\pi}{2}\right)\)
4b.
\(y'=-sinx-1\le0\) ; \(\forall x\in\left(0;2\pi\right)\)
\(\Rightarrow\) Hàm nghịch biến trên \(\left(0;2\pi\right)\)
c.
\(y'=-sinx-\dfrac{1}{sin^2x}+2=\dfrac{-sin^3x+2sin^2x-1}{sin^2x}=\dfrac{\left(sinx-1\right)\left(1-sin^2x+sinx\right)}{sin^2x}\)
\(=\dfrac{\left(sinx-1\right)\left(cos^2x+sinx\right)}{sin^2x}< 0\) ; \(\forall x\in\left(0;\dfrac{\pi}{2}\right)\)
\(\Rightarrow\) Hàm nghịch biến trên \(\left(0;\dfrac{\pi}{2}\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 6 2021
4d.
\(y=cosx+sinx.cosx=cosx+\dfrac{1}{2}sin2x\)
\(y'=-sinx+cos2x=-sinx+1-2sin^2x\)
\(y'=0\Leftrightarrow\left[{}\begin{matrix}sinx=-1\\sinx=\dfrac{1}{2}\end{matrix}\right.\)
\(\Rightarrow x=\left\{\dfrac{\pi}{6};\dfrac{5\pi}{6};\dfrac{3\pi}{2}\right\}\)
Bảng biến thiên
x y' y 0 pi/6 5pi/6 3pi/2 2pi 0 0 0 + - + +
Từ BBt ta thấy hàm đồng biến trên các khoảng \(\left(0;\dfrac{\pi}{6}\right)\) và \(\left(\dfrac{5\pi}{6};2\pi\right)\)
Hàm nghịch biến trên \(\left(\dfrac{\pi}{6};\dfrac{5\pi}{6}\right)\)
4 tháng 9 2021
c: Xét tứ giác AEHF có
\(\widehat{EAF}=\widehat{AFH}=\widehat{AEH}=90^0\)
Do đó: AEHF là hình chữ nhật
Suy ra: AE=HF; AF=HE; AH=EF
Xét ΔAHB vuông tại H có HE là đường cao ứng với cạnh huyền AB
nên \(EA\cdot EB=HE^2\)
hay \(HE^2=EB\cdot HF\)
Xét ΔAHC vuông tại H có HF là đường cao ứng với cạnh huyền AC
nên \(FA\cdot FC=HF^2\)
hay \(HF^2=FC\cdot HE\)
Xét ΔFHE vuông tại H có
\(FE^2=FH^2+EH^2\)
hay \(AH^2=EB\cdot HF+FC\cdot HE\)
15 tháng 11 2021
a: Xét ΔABH và ΔACH có
AB=AC
AH chung
BH=CH
Do đó: ΔABH=ΔACH
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 3 2023
Rút gọn được \(A=\dfrac{\sqrt{x}}{\sqrt{x}-3}\)
\(B-8A\le0\Leftrightarrow\dfrac{x+16}{\sqrt{x}-3}-\dfrac{8\sqrt{x}}{\sqrt{x}-3}\le0\)
\(\Leftrightarrow\dfrac{x-8\sqrt{x}+16}{\sqrt{x}-3}\le0\)
\(\Leftrightarrow\dfrac{\left(\sqrt{x}-4\right)^2}{\sqrt{x}-3}\le0\)
\(\Rightarrow\left[{}\begin{matrix}\sqrt{x}-4=0\\\sqrt{x}-3< 0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=16\\x< 9\end{matrix}\right.\)
Kết hợp ĐKXD ta được: \(\left[{}\begin{matrix}x=16\\0\le x< 9\end{matrix}\right.\)