cho tam giác ABC có 0<B<90 các cạnh BC=a, AC=b, AB=c.
CMR: diện tích tam giác ABC=\(\dfrac{1}{2}\)*AB*BC*\(\sin B\) = \(\dfrac{1}{2}\)*AC*\(\sin B\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: AB → = (−a; b; 0) và AC → = (−a; 0; c)
Vì AB → . AC → = a 2 > 0 nên góc ∠ BAC là góc nhọn.
Lập luận tương tự ta chứng minh được các góc ∠ B và ∠ C cũng là góc nhọn.

Tọa độ trọng tâm G của ΔABC là \(G\left(1;\dfrac{m}{3}\right)\)
⇒ \(\left\{{}\begin{matrix}\overrightarrow{AG}=\left(2;\dfrac{m}{3}\right)\\\overrightarrow{BG}=\left(-3;\dfrac{m}{3}\right)\end{matrix}\right.\)
Để ΔGAB vuông tại G
⇒ GA ⊥ GB
⇒ \(\overrightarrow{GA}\) ⊥ \(\overrightarrow{GB}\)
⇒ \(\overrightarrow{GA}.\overrightarrow{GB}=0\)
⇒ 2 . (-3) + \(\dfrac{m^2}{9}\) = 0
⇒ m2 = 6 . 9 = 54
⇒ m = \(\pm\sqrt{54}\)
Mình chắc chắn cách làm của mình là đúng còn về tính toán thì chưa chắc nên bạn tự kiểm tra nhá ![]()

\(C\in CK\Rightarrow C\left(x;-\dfrac{3}{8}x-\dfrac{13}{8}\right)\)
\(\Rightarrow\overrightarrow{BC}=\left(x+4;-\dfrac{3}{8}x-\dfrac{53}{8}\right)\)
AH có VTPT là \(\overrightarrow{n}=\left(5;3\right)\)
Do \(AH\) vuông góc \(BC\Rightarrow\overrightarrow{BC}=k\overrightarrow{n}\)
\(\Rightarrow\left\{{}\begin{matrix}x+4=5k\\-\dfrac{3}{8}x-\dfrac{53}{8}=3k\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=-\dfrac{361}{39}\\k=-\dfrac{41}{39}\end{matrix}\right.\Rightarrow C\left(-\dfrac{361}{39};\dfrac{24}{13}\right)\).
\(A\in AH\Rightarrow A\left(x;-\dfrac{5}{3}x+\dfrac{4}{3}\right)\)
\(\Rightarrow\overrightarrow{BA}=\left(x+4;-\dfrac{5}{3}x-\dfrac{11}{3}\right)\)
\(CK\) có VTPT \(\overrightarrow{n}=\left(3;8\right)\)
Do \(CK\) vuông góc \(AB\Rightarrow\overrightarrow{BA}=k\overrightarrow{n}\)
\(\Rightarrow\left\{{}\begin{matrix}x+4=3k\\-\dfrac{5}{3}x-\dfrac{11}{3}=8k\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=-\dfrac{43}{13}\\k=\dfrac{3}{13}\end{matrix}\right.\Rightarrow A\left(-\dfrac{43}{13};\dfrac{89}{13}\right)\).

a) Do \(\widehat{A}=100^0>90^0\) nên là góc tù, do đó, \(\widehat{A}\) là góc lớn nhất trong tam giác ABC.
\( \Rightarrow \) BC là cạnh lớn nhất của tam giác ABC (do BC đối diện với góc A trong tam giác ABC)
b)
Theo định lí tổng 3 góc trong tam giác ABC, ta có:
\( \Rightarrow \widehat A + \widehat B + \widehat C = {180^o}\)
\( \Rightarrow \widehat C = {180^o} - {100^o} - {40^o} = {40^o}\)
\( \Rightarrow\widehat C = \widehat B = {40^o}\)
\( \Rightarrow \) ABC là tam giác cân tại A.

Gọi tọa độ điểm H(a;b)
Ta có: A H → = a + 1 ; b − 1 , B H → = a ; b − 2 , B C → = 1 ; − 1 , A C → 2 ; 0
Do H là trực tâm tam giác ABC nên:
A C → . B H → = 0 B C → . A H → = 0 ⇒ 2. a + 0. b − 2 = 0 1. a + 1 − 1. b − 1 = 0 ⇒ a = 0 b = 2
Vậy H (0; 2).
Chọn A

Chọn B.
Ta có:
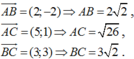
Mặt khác ![]()
Suy ra diện tích tam giác ABC là 1/2.AB.BC = 6.

Ta có:
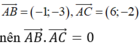
Suy ra tam giác ABC vuông tại A do đó trực tâm H trùng với A
Vậy H( -1 ; 3)
Chọn B.