tìm giá trị n nguyên dương : a) 1/8.16n=2n
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KM
0
T
3
3 tháng 3 2018
Để A nguyên dương
=> n + 1 \(⋮\)2n - 1
Tiếp theo dễ rồi nhé :)
A
3 tháng 3 2018
Để A thuộc N* <=> n+1/2n-1 thuộc N*
Xét 2A= 2n+2/2n-1
Ta cm 2n+2/2n-1 thuộc N*
<=> 2n-1+3/2n-1 thuộc N*
<=> 1+ 3/ 2n-1 thuộc N*
<=> 2n-1 thuộc Ư(3)
Ư(3) = { 1 -1 3 -3 }
=> 2n-1 thuộc {1 -1 3 - 3 }
Sau đó tìm n rồi xét xem với gtri nào của n thì A lớn hơn 0 là xog r đó bạn
TP
4
19 tháng 4 2017
Muốn \(\frac{n^2+2n+1}{n+23}\) có giá trị nguyên thì:
\(n^2+2n+1⋮n+23\Rightarrow n^2+2n+1-n.\left(n+23\right)⋮n+23\)
\(\Rightarrow n^2+2n+1-n^2-23n⋮n+23\)
\(\Rightarrow-21n+1⋮n+23\Rightarrow-21n+1+21\left(n+23\right)⋮n+23\)
\(\Rightarrow-21n+1+21n+23⋮n+23\)
\(\Rightarrow24⋮n+23\Rightarrow n+23\inƯ\left(24\right)\)
Mà n lớn nhất nên: n+23 lớn nhất => n+23 = 24 => n=1
Vậy n = 1
19 tháng 4 2017
Cho mình xin lỗi:
\(-21n+1⋮n+23\Rightarrow-21n+1+21\left(n+23\right)⋮n+23\)
\(\Rightarrow-21n+1+21n+483⋮n+23\Rightarrow484⋮n+23\)
Mà n là số nguyên dương lớn nhất nên: n+23=484 => n = 461
Vậy n = 461
TT
0
22 tháng 4 2015
a) Gọi d là ước nguyên tố của 2n+9/n+1. Ta có:
2n+9-2(n+1) chia hết cho d => d=7
Ta thấy 2n+9 chia hết cho 7 khi đó n+1 chia hết cho 7.
<=> 2n+9-7 chia hết cho 7.
<=>2(n+1) chia hết cho 7 <=> n+1 chia hết cho 7 <=> n=7k-1(k thuộc N)
Vậy nếu n khác 7k-1 thì A là phân số.
7 tháng 1 2023
Để A là số nguyên thì 2n^2-n+4n-2+5 chia hết cho 2n-1
=>\(2n-1\in\left\{1;-1;5;-5\right\}\)
=>\(n\in\left\{1;0;3;-2\right\}\)
H
7 tháng 1 2023
`2n^2+3n+3 | 2n-1`
`-` `2n^2-n` `n+2`
------------------
`4n+3`
`-` `4n-2`
------------
`5`
`<=> (2n^2+3n+3) : (2n-1)=5`
`<=> 5 ⋮ (2n-1)=> 2n-1 ∈ Ư(5)`\(=\left\{1,5\right\}\)
`+, 2n-1=1=>2n=2=>n=1`
`+, 2n-1=-1=>2n=0=>n=0`
`+, 2n-1=5=>2n=6=>n=3`
`+,2n-1=-5=>2n=-4=>n=-2`
vậy \(n\in\left\{1;0;3;-2\right\}\)
PD
0
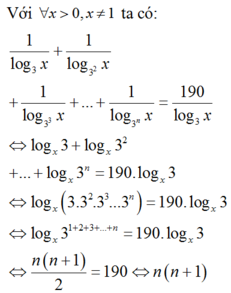
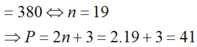
\(\frac{1}{8}.16^n=2^n\)
\(\frac{1}{2^3}.\left(2^4\right)^n=2^n\)
\(\frac{1}{2^3}.2^{4n}=2^n\)
\(\frac{1}{2^3}=2^n:2^{4n}\)
\(\frac{1}{2^3}=2^{n-4n}\)
\(\frac{1}{2^3}=2^{n\left(1-4\right)}\)
\(\frac{1}{2^3}=2^{\left(-3\right)n}\)
\(2^{\left(-3\right)n}.2^3=1\)
\(2^{\left(-3\right)n+3}=1\)
\(2^{3\left(-n+1\right)}=2^0\)
\(\Rightarrow3\left(-n+1\right)=0\)
\(\Rightarrow-n+1=0\)
\(-n=-1\)
\(n=1\)