Có hai cốc thủy tinh trong suốt chứa cùng một lượng nước ở chính giữa cốc. Người ta đổ rượu vào một cốc, cốc còn lại đổ dầu hỏa vừa vặn tới miệng cốc. Điều gì xảy ra nếu chiếu lần lượt một tia sáng hẹp (theo phương bất kì) vào mỗi cốc? Dựa vào kiến thức đã học dự đoán đường đi của mỗi tia sáng trong mỗi cốc chứa đầy các chất lỏng trên.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cốc đựng nước và cốc đựng rượu:
- Đường đi của tia sáng qua cốc 1 là đường thẳng. Vì ánh sáng truyền qua môi trường trong suốt , đồng tính
Cốc đựng dầu và nước:
. Vì dầu hỏa và nước trộn lại không còn đồng tính và trong suốt nữa.
->Ánh sáng không đi theo đường thẳng nữa

Cốc đựng nước và rượu gọi là cốc 1
-đường đi của tia sáng qua cốc 1 là đường thẳng. Vì ánh sáng truyền qua môi trường trong suốt , đồng tính nhưng nước và rượu đồng tình vì có màu trắng trong suốt.
==> áng sáng truyền qua theo đường thẳng( chú ý trong trường hợp này rượu có màu trắng trong, chứ không phải là rượu vang nha)
Cốc đựng dầu hỏa và nước là cốc gọi là cốc 2
-đường đi của ánh sáng qua cốc 2 không còn là đường thẳng nữa . Vì áng sáng không truyền qua môi trường không đồng tính và không trong suốt. Dầu hỏa và nước trộn lại không còn đồng tính và trong suốt nữa.
==> ánh sáng truyền qua không còn thẳng nữa

gọi n là nồng độ của trà 1 lúc ban đầu
\(n2=\dfrac{\Delta m.n}{\Delta m+m2}=\dfrac{n}{1+\dfrac{m2}{\Delta m}}\left(1\right)\)
thay \(x2=\dfrac{\Delta m}{m2}\)
thay vào trường hợp 1 ta có \(n2=\dfrac{n}{1+\dfrac{1}{x2}}=\dfrac{n.x2}{x2+1}\)
nếu trường hợp đổ trở lại m từ cốc 2 sang cốc 1thì nồng độ nước trà cốc 1
\(n1=\dfrac{\left(m1-\Delta m\right).n+\Delta m.n2}{\left(m1-\Delta m\right)+\Delta m}=\dfrac{\left(m1-\Delta m\right).n+\Delta m.\dfrac{n.x2}{x2+1}}{m1}=n-\dfrac{\Delta m.n}{m1}+\dfrac{\Delta m}{m1}.\dfrac{n.x2}{x2+1}\left(2\right)\)
thay \(x1=\dfrac{\Delta m}{m1}\)
vào trường hợp 2 ta có:\(n1=\left(1-x1\right).n+\dfrac{x1.x2.n}{x2+1}\)
theo giả thiết ta có:\(n1=k.n2\)
hay \(\left(1-x1\right).n+\dfrac{x1.x2.n}{x2+1}=k.\dfrac{n.x2}{x2+1}\)
\(1-x1=\dfrac{\left(k-x1\right).x2}{x2+1}\)
suy ra độ chênh lệch giữa hai cốc:\(k=\dfrac{\left(1-x1\right).\left(1+x2\right)}{x2}+x1=\dfrac{1+x2-x1-x1x2}{x2}+x1=\dfrac{1-x1}{x2}+1\left(3\right)\)
\(< =>\dfrac{1-x1}{x2}=k-1=2,5-1=1,5< =>1=1,5x2+x1\left(4\right)\)
khi đổ nước có khối lượng m từ bình 1 sang bình 2 ta có phương trình cân bằng nhiệt
m.c(t1-t)=m2.c(t-t2)
\(t=\dfrac{\Delta m.c.t1+m2.c.t2}{\Delta m.c+m2.c}=\dfrac{\Delta m.t1+m2.t2}{\Delta m+m2}\)
thêm bớt m2t1 vào tử ta có
\(t=\dfrac{\Delta m.t1+m2.t1+m2.t2-m2.t1}{\Delta m+m2}=t1+\dfrac{m2.\left(t2-t1\right)}{\Delta m+m2}=t1+\dfrac{t2-t1}{x2+1}=t1-\dfrac{t2-t1}{x2+1}\left(6\right)\)
khi đổ m trở lại cốc 1 ta có phương trình cân bằng nhiệt sau
m.c(t'-t)=(m1-m).c(t1-t')
\(=>t'=\dfrac{\Delta m.c.t+\left(m1-\Delta m\right)c.t1}{\Delta m.c\left(m1-\Delta m\right)c}=\dfrac{\Delta m.t+\left(m1-\Delta m\right).t1}{m1}< =>t'=x1.t+t1-x1.t1=x1\left(t-t1\right)+t1\)
thay vào trường hợp 6 ta có:\(t'=\left(t1-\dfrac{t1-t2}{x2+1}\right).x1+t1=t1-\dfrac{x1.\left(t1-t2\right)}{x2+1}\left(< >\right)\)
hiệu nhiệt độ giữa hai cốc
\(t=t'-t=t1-\dfrac{x1.\left(t1-t2\right)}{x2+1}-t1-\dfrac{t1-t2}{x2+1}=\dfrac{t1-t2-x1.\left(t1-t2\right)}{x2+1}=\dfrac{\left(1-x1\right).\left(t1-t2\right)}{x2+1}\left(\backslash\right)\)
thay t1,t2,t vào (/) ta có \(15=\dfrac{\left(1-x1\right).\left(45-5\right)}{x2+1}=>15x2+40x1=25\left(\backslash\backslash\right)\)
giải hệ phương trình từ (4) và (\\) ta có: ta được x1=\(\dfrac{1}{2}\)
x2=\(\dfrac{1}{3}\)
ta thấy khi m tăng thì \(x1=\dfrac{\Delta m}{m1}\)
x2=\(\dfrac{\Delta m}{m2}\)
đều tăng ,do đó từ phần (3) và (//) ta có k và t đều giảm

\(p=d\cdot h=10000\cdot0,24=2400Pa\)
\(p'=d\cdot h'=10000\cdot\left(0,24-0,04\right)=2000Pa\)

Đáp án C
Chuẩn hóa bán kính của viên bi là 1 => Chiều cao của cốc là h = 2.
+) Thể tích của viên bi là V 1 = 4 π 3 . Gọi R, r lần lượt là bán kính của miệng cốc và đáy cốc.
+) Thể tích của cốc ( khối nón cụt ) là V 2 = πh 3 R 2 + R r + r 2 = 2 π 3 R 2 + R r + r 2
 +) Vì lượng nước tràn ra bằng nửa lượng nước đổ vào cốc
V
1
V
2
=
1
2
⇒
R
2
+
R
r
+
r
2
=
4
(
1
)
+) Vì lượng nước tràn ra bằng nửa lượng nước đổ vào cốc
V
1
V
2
=
1
2
⇒
R
2
+
R
r
+
r
2
=
4
(
1
)
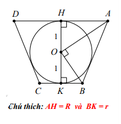
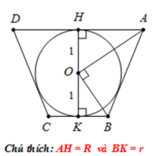
+) Xét mặt cắt của cốc khi thả viên bi vào trong cốc ( hình vẽ bên)
Dễ thấy ABCD là hình thang cân ⇒ O A 2 + O B 2 = A B 2 ( 2 )
Mà O A 2 = R 2 + 1 O B 2 = r 2 + 1 và A B 2 = A H - B K 2 + H K 2 = R - r 2 + 4 ( 3 )
Từ (2) và (3) ⇒ R 2 + r 2 + 2 = R - r 2 + 4 ⇔ R r = 1 ( 4 )
Từ (1) và (4) ⇒ R 2 + R r + r 2 = 4 R r ⇔ R r 2 = 3 R r + 1 = 0
⇔ R r = 3 + 5 2 . Vậy tỉ số cần tính là 3 + 5 2

Đáp án C.

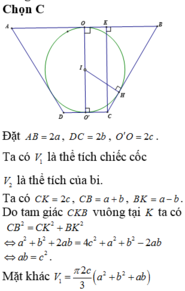
Ta có
V b i = V m c = 4 3 h 2 3 . π ; V c o c = V n c = π 3 . h . R 2 + r 2 + R r
Mà V n c = 2 V m c do vậy π 3 h R 2 + r 2 + R r = 2. 4 3 . h 2 3 π
⇔ R 2 + r 2 + R . r = h 2
Mà ⇔ R 2 + r 2 + R . r = h 2 do vậy
P T ⇔ r R 2 − 3 r R + 1 = 0 ⇔ r R = 3 + 5 2 t m r R = 3 − 5 2 l
Vậy ta chọn C.






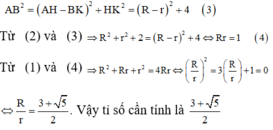
Rồi bắt đầu nè
Ở đây ta phải ứng dụng định luật truyền thẳng của a/s chắc cái này linh thuộc rồi :) thì ta phải xét đến 2 yếu tố trong suốt và đồng tính. Theo bài này thi ta xét theo yếu tố đồng tính
Ở cốc thứ nhất, ta có rượu và nước đều trong suốt( xét yếu tố đồng tính) ta thấy khi rượu mix với nước thì gần như hoà tan với nhau. Ok ➝ ánh sáng ở đây truyền thẳng.
Tương tự ta xét với cốc thứ hai, do nước và dầu hỏa ko hoà tan với nhau nên sẽ tạo ra một mặt phân cách ➝ ánh sáng ở đây sẽ truyền gấp khúc(cụ thể là 1 lần).
Vậy.....
Chúc Linh học ko tốt :))))
Linh ơi